Enoncé
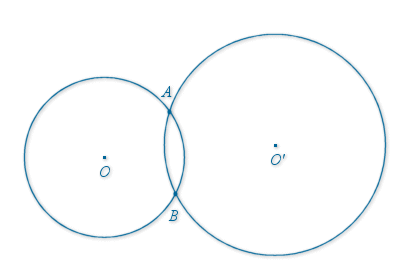
2) ![]() et
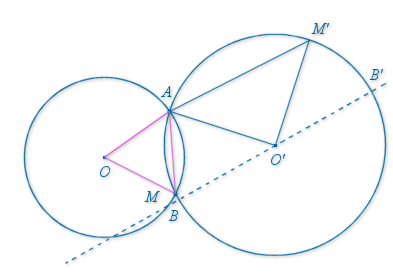
et ![]() sont deux cercles de centres
sont deux cercles de centres
 et
et
 , et de rayons
, et de rayons
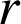 et
et
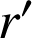 ,
,
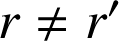 .
. ![]() et
et ![]() ont deux points d'intersection distincts
ont deux points d'intersection distincts
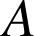 et
et
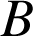 .
.
On appelle
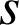 la similitude de centre
la similitude de centre
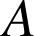 transformant
transformant ![]() en
en ![]() . On pose
. On pose ![]() , et pour tout point
, et pour tout point
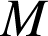 de
de ![]() ,
, ![]() .
.
Résultat
Correction
Explications
A.
La similitude de centre
 transformant
transformant ![]() en
en ![]() a pour rapport
a pour rapport ![]() et transforme
et transforme
 en
en
 . L'angle de la similitude est l'angle
. L'angle de la similitude est l'angle ![]() qui n'est pas un angle droit, sauf cas particulier.
qui n'est pas un angle droit, sauf cas particulier.
B.
La similitude directe
 transforme
transforme
 en
en
 ,
,
 en
en
 , et
, et
 en
en
 . Comme similitude directe, elle conserve les angles orientés et donc
. Comme similitude directe, elle conserve les angles orientés et donc ![]() .
.
Consultez la figure animée suivante.
C.
Si
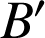 est le point diamétralement opposé à
est le point diamétralement opposé à
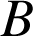 sur
sur ![]() , alors l'angle
, alors l'angle ![]() . Comme l'angle
. Comme l'angle ![]() est égal à l'angle de similitude
est égal à l'angle de similitude ![]() , alors
, alors ![]() est un angle droit. Ceci est en général faux.
est un angle droit. Ceci est en général faux.
D.
Consultez la figure animée suivante.
Démonstration géométrique :
Les triangles
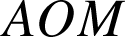 et
et
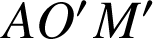 sont directement semblables. On a donc
sont directement semblables. On a donc ![]() et de l'égalité
et de l'égalité ![]() on tire :
on tire : ![]() .
.
Comme de plus ![]() , les triangles
, les triangles
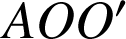 et
et
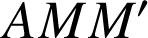 sont directement semblables et donc :
sont directement semblables et donc : ![]() .
.
Pour des raisons de symétrie ![]() et
et ![]() (angle inscrit et angle au centre interceptant le même arc).
(angle inscrit et angle au centre interceptant le même arc).
Donc ![]() , et par conséquent les points
, et par conséquent les points
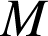 ,
,
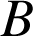 et
et
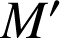 sont alignés.
sont alignés.
Démonstration avec les nombres complexes :
On considère le plan rapporté à un repère d'axe réel
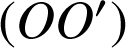 . Dans lequel
. Dans lequel
 a pour affixe
a pour affixe
 et
et
 a pour affixe
a pour affixe
 , avec
, avec
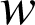 réel. Supposons que
réel. Supposons que
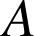 ait pour affixe
ait pour affixe
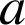 , alors
, alors
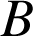 a pour affixe
a pour affixe ![]() .
.
L'angle de la similitude
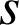 est l'angle
est l'angle 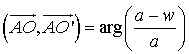 , et le rapport est
, et le rapport est 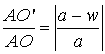 .
.
L'écriture complexe de la similitude est :
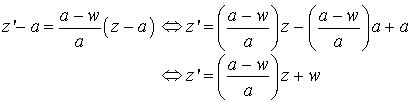
Soit
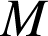 un point de
un point de ![]() , différent de
, différent de
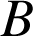 . Son affixe
. Son affixe
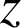 vérifie
vérifie ![]() . Si
. Si
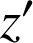 est l'affixe de
est l'affixe de
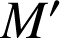 , alors :
, alors :
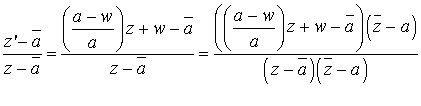
Le dénominateur est réel.
Calculons le numérateur :
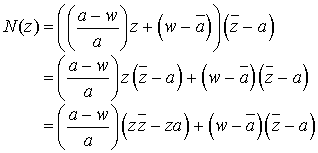
Or ![]() et
et ![]() , donc
, donc ![]() .
.
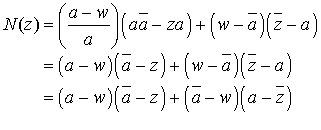
Or
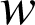 est réel, donc
est réel, donc ![]() et
et ![]() sont conjugués, ce qui montre que
sont conjugués, ce qui montre que ![]() est réel.
est réel.
Il s'ensuit que ![]() est réel donc que l'angle :
est réel donc que l'angle : 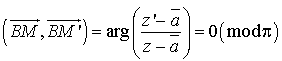 .
.
Les points
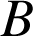 ,
,
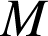 et
et
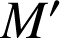 sont alignés.
sont alignés.