Enoncé
1)
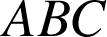 est un triangle, rectangle en
est un triangle, rectangle en
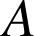 , non isocèle, et
, non isocèle, et
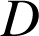 est le projeté orthogonal de
est le projeté orthogonal de
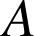 sur
sur
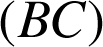 . Le triangle
. Le triangle
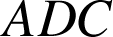 a la même orientation que
a la même orientation que
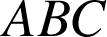 .
.
Résultat
Correction
Explications
A.
Les angles ![]() et
et ![]() sont égaux (angles droits).
sont égaux (angles droits).
Dans le triangle
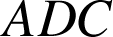 , les angles ont une somme de
, les angles ont une somme de
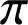 radians :
radians : ![]() .
.
Dans le triangle
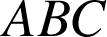 , les angles ont une somme de
, les angles ont une somme de
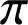 radians :
radians : ![]() .
.
Or ![]() et
et ![]() . Donc
. Donc ![]() .
.
On a donc ![]() . Donc les triangles
. Donc les triangles
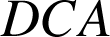 et
et
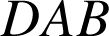 sont (directement) semblables.
sont (directement) semblables.
La similitude directe
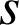 qui transforme
qui transforme
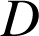 en
en
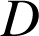 ,
,
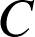 en
en
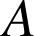 et
et
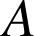 en
en
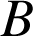 a pour angle
a pour angle ![]() .
.
Par cette similitude, le centre de gravité du triangle
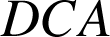 a pour image le centre de gravité du triangle
a pour image le centre de gravité du triangle
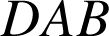 .
.
On a donc ![]() et par conséquent
et par conséquent ![]() est égal à l'angle de similitude soit
est égal à l'angle de similitude soit ![]() .
.
B.
Consultez la figure animée suivante (cliquez ici)
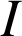 et
et
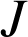 étant les centres de gravité des triangles
étant les centres de gravité des triangles
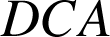 et
et
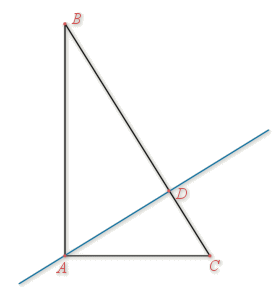
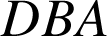 , la droite
, la droite
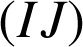 coupe
coupe
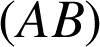 et
et
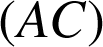 en
en
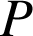 et
et
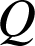 .
.
Soit
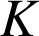 le milieu de
le milieu de
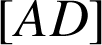 . L'homothétie de centre
. L'homothétie de centre
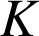 et de rapport
et de rapport
 transforme
transforme
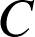 en
en
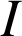 et
et
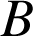 en
en
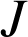 . L'image par cette homothétie de la droite
. L'image par cette homothétie de la droite
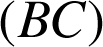 est la droite
est la droite
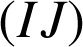 qui lui est donc parallèle.
qui lui est donc parallèle.
Les triangles
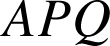 et
et
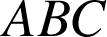 sont semblables, et comme
sont semblables, et comme
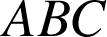 n'est pas isocèle, le triangle
n'est pas isocèle, le triangle
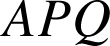 n'est pas isocèle.
n'est pas isocèle.
C.
Consultez la figure animée suivante (cliquez ici)
Par la similitude
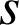 décrite dans la proposition A, l'image du centre du cercle inscrit dans un triangle est le centre du cercle inscrit dans le triangle image (la similitude conserve les angles, donc les bissectrices). On a donc, comme dans la proposition A,
décrite dans la proposition A, l'image du centre du cercle inscrit dans un triangle est le centre du cercle inscrit dans le triangle image (la similitude conserve les angles, donc les bissectrices). On a donc, comme dans la proposition A, ![]() .
.
![]() est égal à l'angle de similitude soit
est égal à l'angle de similitude soit ![]() .
.
D.
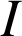 et
et
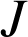 étant les centres des cercles inscrits des triangles
étant les centres des cercles inscrits des triangles
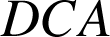 et
et
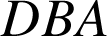 , la droite
, la droite
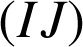 coupe
coupe
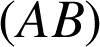 et
et
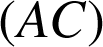 en
en
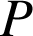 et
et
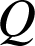 .
.
La similitude
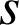 introduite dans la proposition
introduite dans la proposition
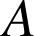 , a pour rapport
, a pour rapport ![]() et transforme
et transforme
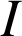 en
en
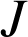 .
.
On a donc : ![]() . Donc
. Donc ![]() .
.
De plus ![]() . Donc les triangles
. Donc les triangles
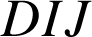 et
et
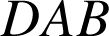 sont directement semblables, et la similitude
sont directement semblables, et la similitude
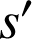 qui transforme
qui transforme
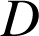 en
en
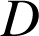 ,
,
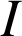 en
en
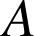 et
et
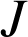 en
en
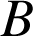 a pour angle
a pour angle ![]() , car la droite
, car la droite
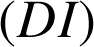 est bissectrice de l'angle
est bissectrice de l'angle ![]() .
.
L'image par
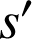 de la droite
de la droite
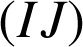 est la droite
est la droite
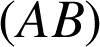 . On a donc
. On a donc ![]() .
.
Le triangle
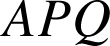 est rectangle en
est rectangle en
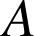 , et il a un angle de
, et il a un angle de ![]() . Il est donc isocèle.
. Il est donc isocèle.
Consultez la figure animée suivante (cliquez ici).