Enoncé
2) On considère dans le plan orienté un triangle rectangle isocèle
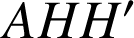tel que 
modulo 
.
On appelle 
la droite 
.
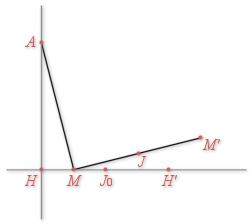
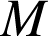est un point quelconque de la droite et
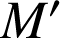le point tel que le triangle
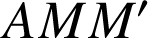est rectangle isocèle et vérifie 
modulo .
est le milieu de 
et 
est le milieu de 
.
Pour répondre aux questions, vous pouvez vous aider de la figure suivante (cliquez ici), sur laquelle vous pouvez déplacer le point
à l'aide de la souris.
Résultat
Correction
Explications
A.
Le triangle
est rectangle isocèle direct, donc :
,
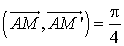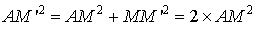et 
.
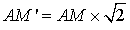La similitude de centre
qui transforme
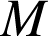en
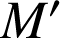a pour angle 
, mais elle a pour rapport 
.
B.
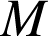parcourt la droite . Donc
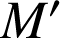appartient à l'image de cette droite par la similitude de centre
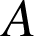qui transforme
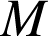en
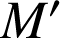. Consultez la figure animée suivante (cliquez ici).
Pour en savoir plus...
Soit
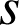cette similitude.
Par construction, l'image de
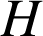est
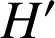. L'image de
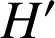est le point
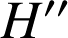tel que
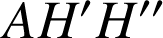soit rectangle isocèle en
, avec 
.
L'image de par
est la droite 
.
Réciproquement,
étant bijective, tout point de 
est l'image d'un point
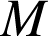de .
Le lieu géométrique de
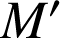lorsque
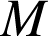parcourt est la droite .
C.
Consultez la figure animée suivante (cliquez ici).
La similitude de centre
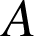, d'angle 
et de rapport 
transforme le triangle
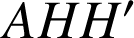en
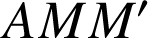(car l'image d'un triangle rectangle isocèle direct est un triangle rectangle isocèle direct).
Elle envoie , milieu de , en
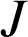, milieu de (conservation du milieu par la similitude). Par conséquent :
et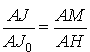 
, d'où l'on tire :
et 
.
La similitude
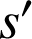de centre
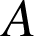, d'angle 
et de rapport 
transforme :
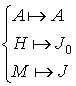
Donc les triangles
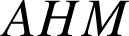et 
sont semblables.
D.
La similitude
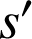de centre
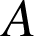, d'angle et de rapport transforme
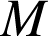en
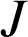(voir corrigé de la proposition C).
Le lieu de
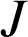lorsque
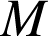parcourt est donc , la droite image de par
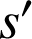(consultez la figure animée suivante).