Enoncé
1)
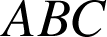 est un triangle direct du plan orienté.
est un triangle direct du plan orienté.
On désigne respectivement par
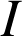 ,
,
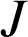 et
et
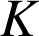 les milieux de
les milieux de ![]() ,
, ![]() et
et ![]() .
.
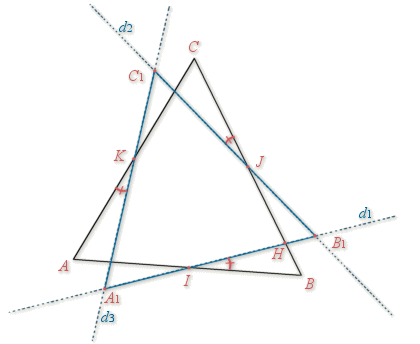
Soit
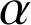 un réel.
un réel.
![]() est l'image de la droite
est l'image de la droite ![]() par la rotation de centre
par la rotation de centre
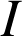 et d'angle
et d'angle
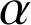 .
.
![]() est l'image de la droite
est l'image de la droite ![]() par la rotation de centre
par la rotation de centre
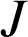 et d'angle
et d'angle
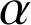 .
.
![]() est l'image de la droite
est l'image de la droite ![]() par la rotation de centre
par la rotation de centre
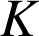 et d'angle
et d'angle
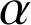 .
.
![]() est le point d'intersection de
est le point d'intersection de ![]() et
et ![]() , celui de
, celui de ![]() et
et ![]() et
et ![]() celui de
celui de ![]() et
et ![]() .
.
On appelle
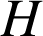 le point d'intersection de
le point d'intersection de ![]() et
et ![]() . On suppose que le choix de
. On suppose que le choix de
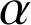 garantit l'existence de ce point.
garantit l'existence de ce point.
Pour répondre aux questions vous pouvez vous aider de la figure suivante (cliquez ici), sur laquelle vous pouvez :
déplacer les points à l'aide de la souris,
fixer vous même l'angle
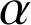 .
.
Résultat
Correction
Explications
A.
Exhibons une situation où les triangles n'ont manifestement pas les mêmes angles.
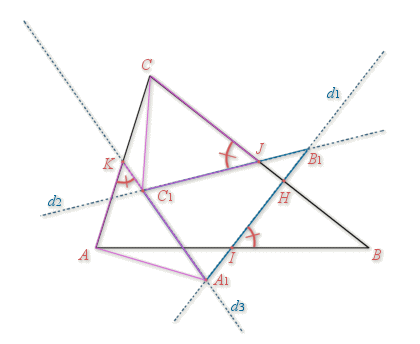
Vous pouvez visualiser la figure animée suivante (cliquez ici) et fixer vous même l'angle
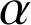 sur cette figure.
sur cette figure.
B.
Les triangles
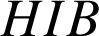 et ont deux angles deux à deux égaux :
et ont deux angles deux à deux égaux :
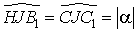 (angles opposés par le sommet) et
(angles opposés par le sommet) et 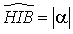 donc
donc 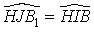 .
.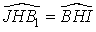 (opposés par le sommet).
(opposés par le sommet).
Donc ils sont semblables.
C.
On peut déduire du fait que les triangles
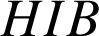 et
et ![]() sont semblables que les angles
sont semblables que les angles ![]() et
et ![]() sont égaux, c'est-à-dire que les angles
sont égaux, c'est-à-dire que les angles ![]() et
et ![]() sont égaux. On pourrait montrer de même que les autres angles des triangles
sont égaux. On pourrait montrer de même que les autres angles des triangles
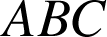 et
et ![]() sont égaux, donc ces triangles sont bien semblables.
sont égaux, donc ces triangles sont bien semblables.
D.
Sur la figure dynamique suivante (cliquez ici), vous pouvez choisir la valeur de
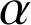 avec la souris.
avec la souris.
Dans la situation particulière où ![]() ,
, ![]() ,
, ![]() et
et ![]() sont les médiatrices du triangle
sont les médiatrices du triangle
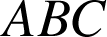 et les points
et les points ![]() ,
, ![]() et
et ![]() sont confondus avec le centre du cercle circonscrit au triangle
sont confondus avec le centre du cercle circonscrit au triangle
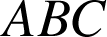 . Dans ces conditions les distances
. Dans ces conditions les distances ![]() ,
, ![]() et
et ![]() sont nulles et ne peuvent être égales aux distances
sont nulles et ne peuvent être égales aux distances
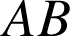 ,
,
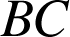 et
et
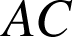 .
.