1
/
2
1)
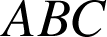 est un triangle direct du plan orienté.
est un triangle direct du plan orienté.
On désigne respectivement par
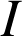 ,
,
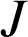 et
et
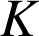 les milieux de
les milieux de ![]() ,
, ![]() et
et ![]() .
.
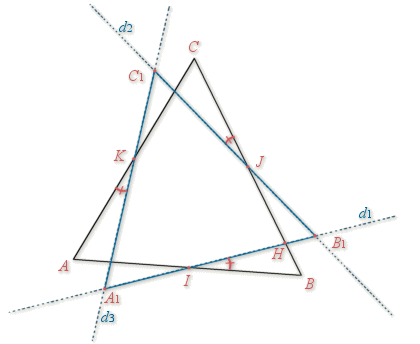
Soit
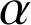 un réel.
un réel.
![]() est l'image de la droite
est l'image de la droite ![]() par la rotation de centre
par la rotation de centre
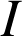 et d'angle
et d'angle
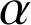 .
.
![]() est l'image de la droite
est l'image de la droite ![]() par la rotation de centre
par la rotation de centre
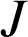 et d'angle
et d'angle
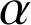 .
.
![]() est l'image de la droite
est l'image de la droite ![]() par la rotation de centre
par la rotation de centre
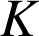 et d'angle
et d'angle
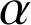 .
.
![]() est le point d'intersection de
est le point d'intersection de ![]() et
et ![]() , celui de
, celui de ![]() et
et ![]() et
et ![]() celui de
celui de ![]() et
et ![]() .
.
On appelle
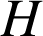 le point d'intersection de
le point d'intersection de ![]() et
et ![]() . On suppose que le choix de
. On suppose que le choix de
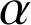 garantit l'existence de ce point.
garantit l'existence de ce point.
Pour répondre aux questions vous pouvez vous aider de la figure suivante (cliquez ici), sur laquelle vous pouvez :
déplacer les points à l'aide de la souris,
fixer vous même l'angle
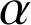 .
.