Enoncé
10) Étant donnés deux cercles ![]() et
et ![]() sécants et de rayons distincts
sécants et de rayons distincts
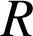 et
et
 , il existe une similitude directe et une seule transformant
, il existe une similitude directe et une seule transformant ![]() en
en ![]() .
.
Résultat
Correction
Explications
Toute similitude de rapport ![]() et transformant
et transformant
 en
en
 convient. On peut donner les exemples suivants :
convient. On peut donner les exemples suivants :
Les droites ![]() et
et ![]() sont parallèles. On considère alors l'homothétie de centre
sont parallèles. On considère alors l'homothétie de centre
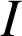 et de rapport
et de rapport ![]() , ainsi que l'homothétie de centre
, ainsi que l'homothétie de centre
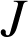 et de rapport
et de rapport ![]() .
.
La similitude de centre
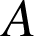 , de rapport
, de rapport ![]() et d'angle
et d'angle ![]() convient.
convient.
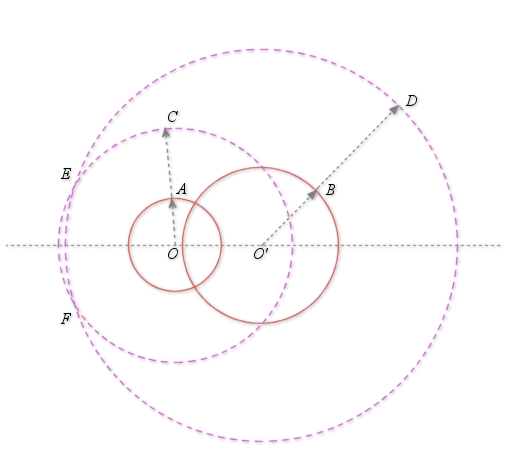
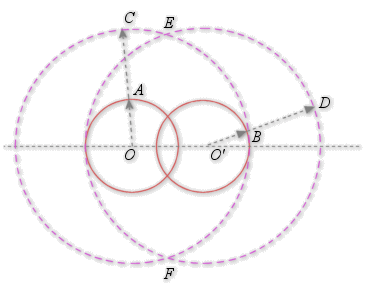
 est un réel. (sur la figure
est un réel. (sur la figure
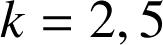 ). On a construit les cercles de centre
). On a construit les cercles de centre
 et
et
 et de rayons respectifs
et de rayons respectifs
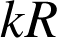 et
et
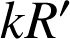 .
.
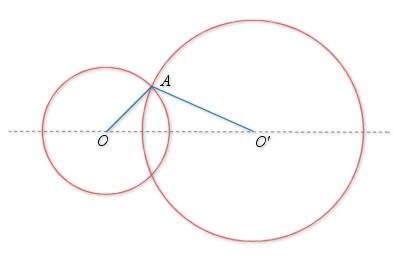
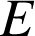 étant un point d'intersection des deux cercles,
étant un point d'intersection des deux cercles, ![]() et
et ![]() . Donc
. Donc ![]() et la similitude de centre
et la similitude de centre
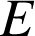 , de rapport
, de rapport ![]() et d'angle
et d'angle ![]() transforme
transforme
 en
en
 et donc
et donc ![]() en
en ![]() .
.
Remarque : si
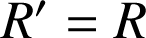 , la construction précédente convient : donc il existe une rotation transformant
, la construction précédente convient : donc il existe une rotation transformant ![]() en
en ![]() . Dans ce cas, la translation de vecteur
. Dans ce cas, la translation de vecteur ![]() convient également.
convient également.