Enoncé
9) Soit
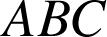 un triangle ; il existe une similitude directe et une seule qui transforme
un triangle ; il existe une similitude directe et une seule qui transforme
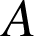 en
en
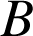 et
et
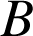 en
en
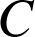 .
.
Résultat
Correction
Explications
Il suffit d'appliquer un théorème du cours.
Rappel : similitude directe transformant deux points distincts
Si
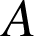 ,
,
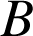 ,
,
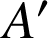 et
et
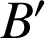 sont quatre points du plan tels que
sont quatre points du plan tels que ![]() et
et ![]() , alors il existe une seule similitude directe
, alors il existe une seule similitude directe
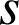 telle que
telle que ![]() et
et ![]() .
.
Le rapport de
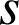 est égal
est égal ![]() , et l'angle est égal à
, et l'angle est égal à ![]() .
.