Enoncé
4)
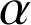étant un réel fixé, si par une transformation
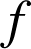, on a :
pour tout couple de points 
: 
,
alors
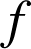est une rotation d'angle
.
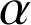Résultat
Correction
Explications
Ce peut être une similitude directe d'angle
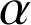mais de rapport
.
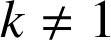Par exemple la similitude directe
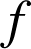d'écriture 
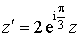, composée de la rotation
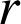de centre
et d'angle 
et de l'homothétie
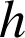de centre
et de rapport
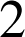, vérifie cette propriété.
En effet soient
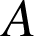et
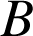deux points quelconques,
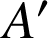et
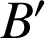leurs images par
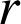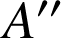et
et
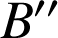les images de
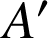et
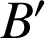par
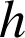. On a :
et 
, et 
(puisque le rapport d'homothétie est positif).
Donc 
.