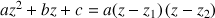Résolution des équations du second degré
Définition :
Considérons l'équation :
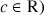
Le discriminant est
.
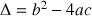Soit
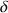un nombre complexe tel que
.
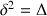L'équation admet deux solutions complexes : 
et 
.
Si
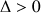, les deux solutions sont réelles.Si
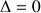, les deux solutions sont confondues (solution réelle double).Si
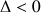, les deux solutions sont complexes conjuguées.
Dans ces conditions : pour tout
:
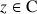