/

Enoncé

8) Soit un entier relatif non nul quelconque. On considère la suite définie par . Que peut-on dire de cette suite ?

Résultat

	A. C'est une suite arithmétique
	B. Elle est croissante
	C. Elle est bornée
	D. Elle contient une infinité de carrés

A. C'est une suite arithmétique

Pour tout entier naturel , .

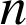est la suite arithmétique de raison et de premier terme .

B. Elle est croissante

Si 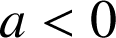, alors la suite est décroissante.

C. Elle est bornée

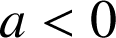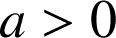Si , alors ; si alors .

D. Elle contient une infinité de carrés

Pour tout entier 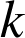, , qui est de la forme .
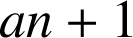