Enoncé
6) Soit
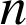un entier naturel non nul.
Posons 
et supposons que 
est premier.
Résultat
Correction
Explications
A. La décomposition de
en produit de facteurs premiers est 
Les facteurs
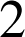et sont bien des nombres premiers et 
.
C.
possède
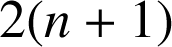diviseurs entiers naturels
possède 
diviseurs. Les diviseurs de
sont : 
avec 
.
D. La somme des diviseurs de
est égale à
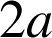
La liste des diviseurs contient deux suites géométriques.
