2) Répondre par vrai ou faux en justifiant.
Si
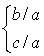 , alors
, alors
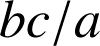 .
.Si
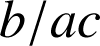 , alors
, alors
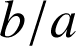 ou
ou
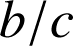 .
.Dans
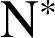 , si
, si
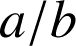 et
et
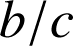 et
et
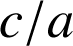 , alors
, alors
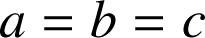 .
.
2) Répondre par vrai ou faux en justifiant.
Si ![]() , alors
, alors
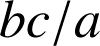 .
.
Si
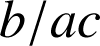 , alors
, alors
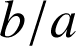 ou
ou
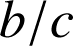 .
.
Dans
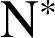 , si
, si
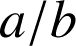 et
et
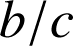 et
et
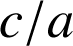 , alors
, alors
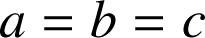 .
.