Le calcul pratique de cette intégrale triple va se ramener au calcul pratique d'une intégrale simple et d'une intégrale double, ou de trois intégrales simples comme on le démontre ci-dessous.

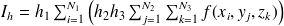
soit en passant à la limite quand 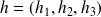tend vers

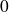
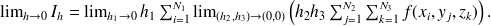
D'où, par définition de l'intégrale simple et de l'intégrale double,

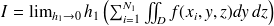
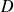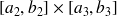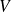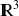où représente le rectangle c'est à dire l'intersection du domaine de avec un plan perpendiculaire avec l'axe 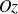. Si l'on pose

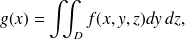
on obtient

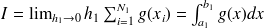
d'où

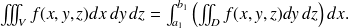
On pourrait démontrer de la même manière, en regroupant différemment les sommes, que

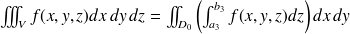
où 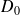représente le rectangle 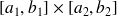, qui peut être considéré aussi comme la projection du domain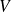e de 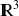sur le plan 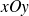. En effet, on aurait

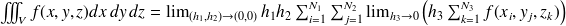
soit

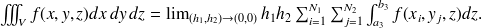
Si l'on pose

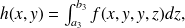
on retrouve la définition de l'intégrale double de 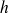sur 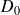, ce qui donne l'équation 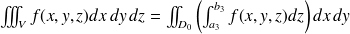. Puisque le calcul d'une intégrale double se ramène au calcul de deux intégrales simples, le calcul de l'intégrale triple se ramène donc au calcul de trois intégrales simples, soit

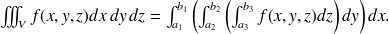
Il est facile de voir que l'on peut écrire les intégrales simples dans n'importe quel ordre puique les bornes de ces intégrales sont indépendantes lorsque le domaine d'intégration est un parallélépipède rectangle.