Soit
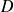 une partie de
une partie de
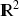 limitée par une courbe fermée, sans point double, parcourue dans le sens direct, notée
limitée par une courbe fermée, sans point double, parcourue dans le sens direct, notée
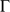 . Soient deux fonctions
. Soient deux fonctions
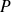 et
et
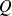 qui admettent des dérivées partielles premières continues sur
qui admettent des dérivées partielles premières continues sur
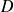 , alors on a :
, alors on a :
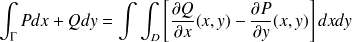
-
Sous les hypothèses précédentes, on peut écrire que :
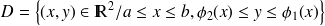
On note
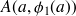 et
et
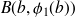 . On a
. On a
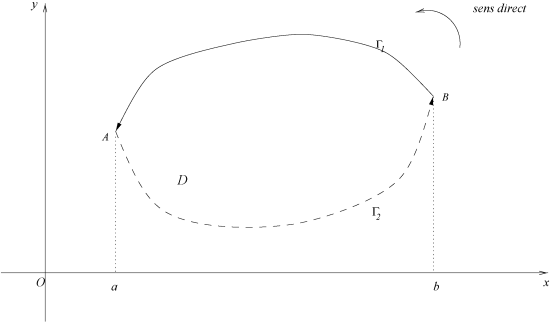
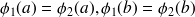 . Voir figure \ref {gr}.
. Voir figure \ref {gr}.Les points de la "frontière''
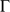 de
de
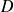 vérifient l'une ou l'autre des équations
vérifient l'une ou l'autre des équations
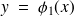 ou
ou
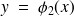 et la courbe
et la courbe
 peut donc être paramétrée en deux "morceaux'' qui se rejoignent en
peut donc être paramétrée en deux "morceaux'' qui se rejoignent en
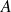 et
et
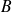 :
: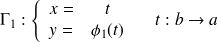
et
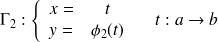
Le parcours de
 dans le sens direct correspond alors bien au parcours de
dans le sens direct correspond alors bien au parcours de
 puis de
puis de
 avec les paramétrages indiqués ci-dessus.
avec les paramétrages indiqués ci-dessus.
-
Calculons l'intégrale double :
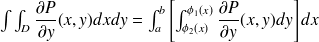
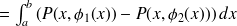
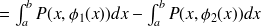
-
Calculons
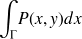 , on écrit cette circulation comme la somme de la circulation sur
, on écrit cette circulation comme la somme de la circulation sur
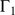 et sur
et sur
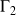 , on utilise la paramétrisation de ces 2 courbes pour calculer ces circulations.
, on utilise la paramétrisation de ces 2 courbes pour calculer ces circulations.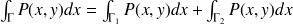
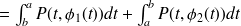
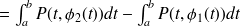
-
On en déduit donc :
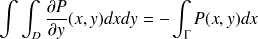
-
De manière analogue, en écrivant la définition de
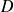 sous la forme :
sous la forme :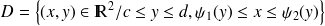
on montrerait que :
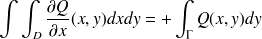
Des deux relations précédentes, on tire la conclusion.