Le théorème de Green-Riemann, peut servir au calcul d'aires. On a vu dans le chapitre sur les intégrales doubles que le calcul de l'aire d'un domaine plan
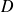se ramène au calcul de l'intégrale double :
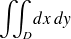. Si on suppose connues les équations explicites du bord de
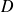sous la forme par exemple:
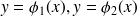, on obtient alors
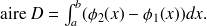
Quand le bord
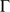de
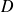est connu non pas par ses équations explicites,
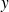en fonction de
ou
en fonction de
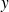, mais par des équations paramétriques, on ne sait pas calculer l'intégrale double ! Le théorème de Green-Riemann est alors utile puisqu'il permet de remplacer le calcul d'une intégrale double sur
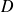par celui d'une intégrale curviligne le long de
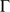, ce dernier calcul s'effectue facilement quand on connaît une paramétrisation de
.
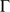Soit
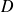une partie de
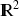limitée par une courbe fermée, sans point double, parcourue dans le sens direct, notée
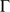, alors on a :
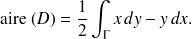
La proposition précédente est à démontrer dans l'exercice de TD n°7.
On a vu qu'un cas particulier de courbes paramétrées dans le plan sont les courbes en polaires. On peut encore utiliser le résultat précédent et on obtient :
Soit
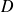une partie de
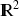limitée par une courbe fermée, sans point double, parcourue dans le sens direct, notée
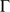dont l'équation polaire est :
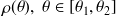, alors on a :
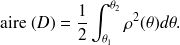
La proposition précédente est à démontrer dans l'exercice de TD n°8.