Si la courbe
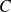est paramétrée par (
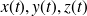), on a vu que lorsque les fonctions sont dérivables et non toutes simultanément nulles, alors le vecteur
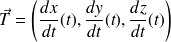est un vecteur tangent à la courbe en
.
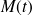Si l'on a défini une abscisse curviligne
sur
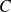on peut paramétrer
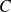à l'aide de
et noter (
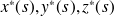) les coordonnées en fonction de l'abscisse curviligne. On a donc :
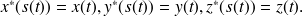
Un autre vecteur tangent est donc donné par
.
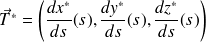En utilisant les résultats sur les fonctions composées, on obtient :
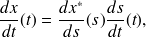
et des relations similaires pour
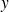et
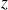. On a donc la relation :
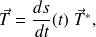
d'où :
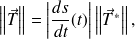
or :
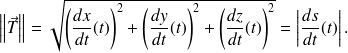
On en déduit donc que
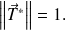
On peut montrer plus précisément :
Soit
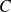une courbe munie d'une abscisse curviligne
(donc d'une orientation), on note
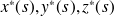les coordonnées des points de
en fonction de
, alors
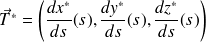est le vecteur tangent à
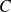en
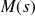, unitaire et dirigé dans le sens de
.
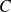