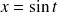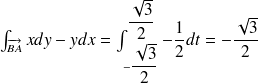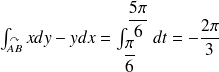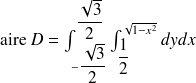On définit
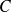l'astroïde d'équation
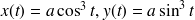. On appelle
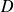l'intérieur de
.
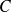Faire un figure représentant
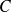et
.
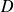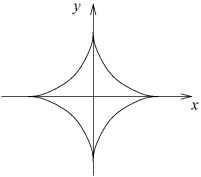
Calculer l'aire de
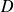en utilisant le théorème de Green-Riemann.
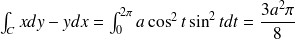
Après linéarisation.
Etait-il possible de calculer l'aire de
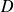en utilisant une intégrale double ?
On ne connaît pas l'équation explicite de l'astroïde.
On définit
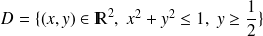, on note
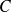le bord de
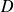orienté dans le sens trigonométrique ditect.
Faire un figure représentant
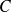et
.
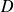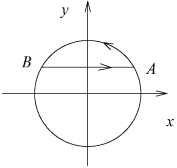
A l'aide de résultats connus sur les aires de triangles et de secteurs de disques, donner l'aire de
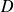. (réponse
)
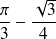L'angle
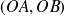vaut
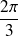, que vaut l'aire du secteur de disque
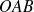. Que vaut l'aire du triangle
?
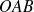aire
=
.
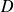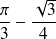Calculer l'aire de
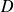en utilisant le théorème de Green-Riemann.
On paramètre le segment
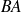, puis l'arc de cercle
.
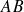Calculer l'aire de
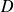en utilisant une intégrale double.
Pour calculer l'intégrale de
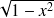, penser au changement de variable
