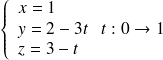On définit le point
, calculer la circulation du champ de vecteurs
de composantes
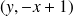le long des courbes suivantes (on précisera l'orientation choisie).
-
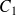est le cercle de centre
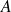de rayon
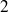, (réponse :
). -
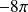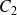est l'arc de
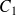situé dans le demi plan
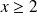, (réponse :
). -
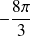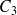est l'arc de
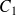situé dans la portion de plan
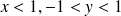, (réponse :
).
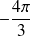Il faut commencer par représenter et paramétrer les courbes
-
:
-
:
-
:
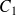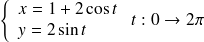
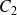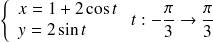
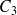Etait-il possible de calculer les circulations précédentes en utilisant le théorème de Green Riemann ?
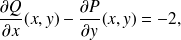
donc la circulation le long de la courbe
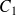vaut
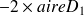si
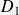est le domaine limité par la courbe fermée
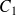. Cette aires se calcule très facilement puisqu'il s'agit d'un disque. Par contre
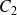et
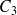ne sont pas fermées, il n'est donc pas possible d'utiliser le théorème de Green-Riemann.
Calculer la circulation du champ de vecteurs
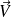le long des courbes définies de la façon suivante (dans chacun des cas faire une figure sur laquelle on représentera la courbe et l'orientation choisie).
-
a pour équations
,
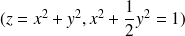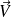a pour composantes
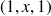; (réponse :
). -
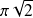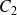a pour équations
,
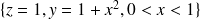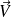a pour composantes
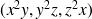; (réponse :
). -
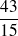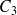est le segment de droite qui joint les points de coordonnées
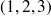et
,
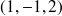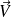a pour composantes
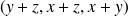; (réponse :
).
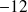Il faut commencer par représenter et paramétrer les courbes :
-
:
-
:
-
:
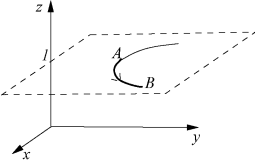
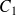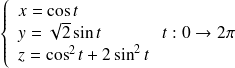
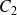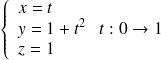
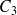