On appelle équation différentielle linéaire du deuxième ordre une équation de la forme
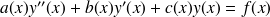
où
,
,
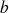et
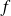sont des fonctions données.
On appelle équation homogène associée à l'équation
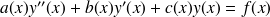l'équation
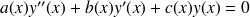
Toute solution de
peut s'écrire sous la forme
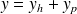
où
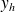est la solution générale de l'équation homogène
et
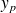est une solution particulière de l'équation "avec second
membre''
.
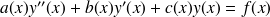La démonstration est à faire en exercice.
Résoudre l'équation
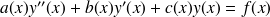consiste donc à déterminer
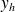et
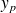. Il n'existe pas de méthode générale pour calculer ces solutions dans le cas où les éléments
,
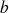et
ne sont pas des constantes. Heureusement, comme le montrent les exemples du paragraphe référencé, ce sont souvent des équations différentielles linéaires du deuxième ordre dans lesquelles
,
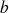et
sont des constantes qui résultent de la modélisation des phénomènes physiques. De telles équations sont dites à coefficients constants et s'écrivent donc
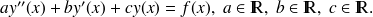
On va voir dans le paragraphe suivant comment trouver la solution générale d'une équation homogène à coefficients constants.