Définition
Soit
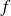une fonction définie sur
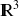qui admet des dérivées partielles secondes, on définit la fonction laplacien par :
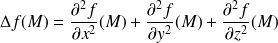
Proposition
Si
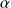est une constante réelle, si
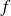et
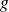sont deux fonctions qui admettent des dérivées partielles secondes, on a :
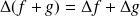
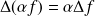
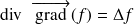
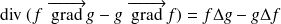
Définition
Soit
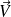un champ de vecteurs dont les composantes
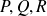admettent des dérivées partielles secondes, on définit le laplacien vectoriel du champ
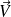par :
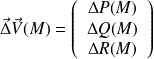
Proposition
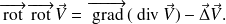
Démontrer la proposition précédente en exercice.