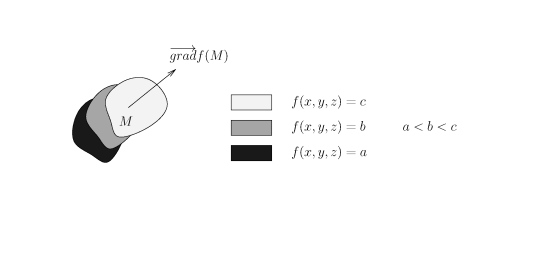
On a vu dans le chapitre "rappels de géométrie" que si
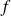est une fonction définie sur
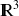, si
est une constante, alors le sous-ensemble de
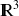, dont l'équation est
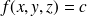, est une surface. Cette surface est appelée surface iso-valeurs.
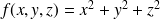Si
, si
est positive, la surface est une sphère centrée en
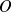. Dans la pratique selon ce que représente la fonction
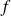, la surface iso-valeur est une isotherme, une équipotentielle, une surface de niveau, etc. On a démontré dans le chapitre "rappels de géométrie" la proposition importante suivante :
Si
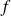est une fonction de 3 variables différentiable, si
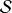est la surface iso-valeurs dont l'équation est :
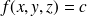, si
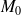est un point de
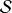alors
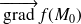(s'il n'est pas nul) est orthogonal à la surface
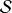en
.
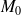La proposition précédente peut être généralisée au cas des fonctions de n variables, en particulier dans le cas
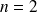, l'ensemble d'équation
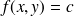est une courbe de
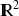, on a la proposition :
Si
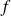est une fonction de 2 variables différentiable, si
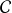est la courbe iso-valeurs dont l'équation est :
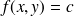, si
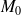est un point de
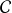alors
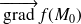(s'il n'est pas nul) est orthogonal à la courbe
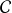en
.
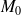Un vecteur est orthogonal à une courbe en un point si ce vecteur est orthogonal au vecteur tangent à la courbe en ce point. Un vecteur est orthogonal à une surface en un point si ce vecteur est orthogonal au plan tangent à la surface en ce point.
On peut compléter les 2 propositions précédentes par un résultat très important en optimisation. Vous pourrez lire une démonstration de cette proposition en document.:
Le vecteur
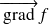, s'il n'est pas nul, est "dirigé suivant les valeurs croissantes" de
.
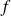La proposition précédente est très importante en optimisation. De nombreux problèmes pratiques se ramènent à une minimisation d'une fonction dite fonction coût, cette fonction dépend en général de plusieurs variables (le nombre peut être très grand).Dans le cas de problèmes complexes faisant intervenir un grand nombre de variables, il n'est pas possible de calculer une solution exacte. On a alors recours à des méthodes numériques, parmi celles-ci certaines sont appelées méthodes du gradient. Elles utilisent en particulier la propriété énoncée dans la proposition précédente.
