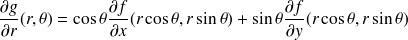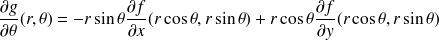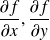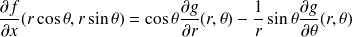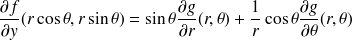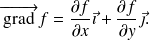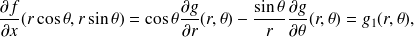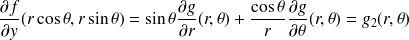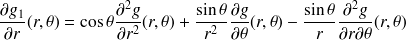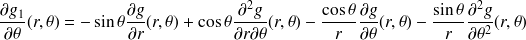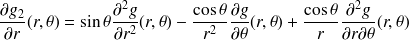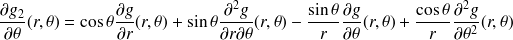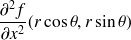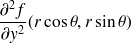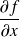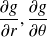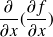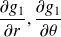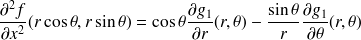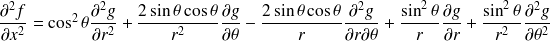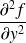Si
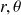sont les coordonnées polaires d'un point
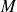de
(
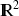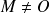), si
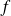est une fonction de 2 variables qui admet des dérivées secondes, on définit la fonction
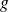par
.
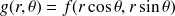Exprimer les dérivées partielles premières de
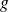à l'aide des dérivées partielles de
.
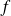Calculer les dérivées partielles de
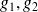par rapport à
et
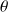à l'aide des dérivées secondes de
.
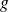En déduire l'expression du laplacien en coordonnées polaires.