Exercice corrigé : équations du second degré
Sujet
Déterminer les solutions de l'équation du second degré
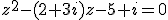
Solution
-
On calcule
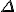
![]()
- On cherche les deux racines de
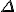 que l'on appellera
que l'on appellera 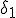 et
et 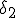 (cf racines d'un nombre complexe )
(cf racines d'un nombre complexe )
Ces racines vérifient
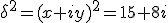
Ce qui permet d'écrire
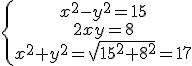
(1) +(3) donne
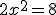
(3)-(1) donne
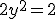
(2) donne x et y sont de même signe
On en déduit les deux racines de
:
et
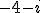
- On en déduit les solutions de l'équation du second ordre