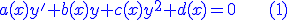MR :Equations différentielles de Ricatti

|
Une équation différentielle de Ricatti est une équation différentielle qui peut s'écrire sous la forme
|
|
Méthode de résolution
- On connaît une solution particulière
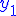 de l'équation différentielle de l'équation différentielle 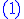
- On cherche alors une solution générale de la forme
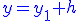
On remplace dans 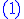 
Ce qui donne :
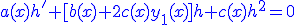
h(x) est solution d'une équation de Bernouilli
|
|
|
Exercice corrigé :
- Résoudre l'équation différentielle définie sur R*
|
|
On reconnaît une équation de Ricatti , 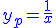 est une solution particulière de est une solution particulière de 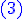
|
|
On cherche une solution de la forme
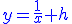
On obtient l'équation différentielle de Bernouilli ci-dessous:
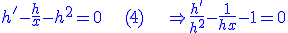
-
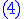 est une équation de Bernouilli que l'on sait résoudre en posant est une équation de Bernouilli que l'on sait résoudre en posant 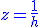
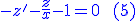
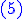 est une équation différentielle linéaire est une équation différentielle linéaire
-
- solution de l'équation sans second membre
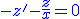
-
-
solution particulière de l'équation complète
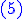
On utilise la méthode de la variation de la constante
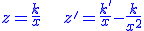
On remplace dans 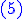 et on obtient et on obtient 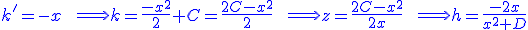
les solutions de l'équation différentielle
|
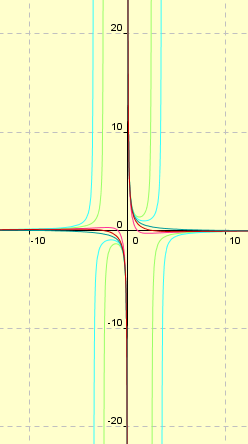
Tracé de quelques solutions de l'équation différentielle
|
|
Si on fixe des conditions initiales
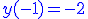
La solution est unique:
|
|