M2LC :Equations différentielles linéaires

Défintion
Une équation différentielle linéaire à coefficients constants est une équation de la forme
 |
|
|
|
Exemple corrigé:
Résoudre l'équation différentielle
|
|
|
est une équation différentielle linéaire à coefficients constants
|
- On cherche l'équation caractéristique et on la résout
-
La solution de l'équation sans second membre est :
- On cherche une solution particulière de l'équation

On remplace dans l'équation différentielle avec second membre (2)
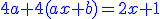
On en déduit :
- La solution générale de l'équation différentielle
est la somme de la solution de l'équation sans second membre et de la solution particulière
|
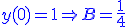
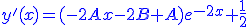
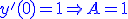
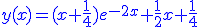
- tracé de la solution de l'équation différentielle avec conditions initiales
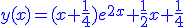
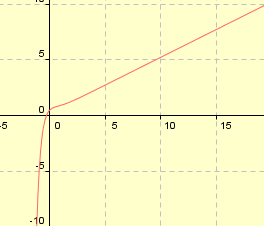
|