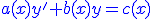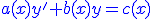M1L: Equations différentielles linéaires

|
Défintion
Une équation différentielle linéaire est une équation de la forme
avec comme conditions:
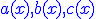 fonctions continues sur un intervalle I de fonctions continues sur un intervalle I de  dans lequel dans lequel 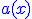 ne s'annule jamais. ne s'annule jamais.
|
|
Cette équation est à variables séparables, sa solution est de la forme :
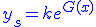 avec avec 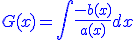
- On détermine une solution particulière
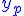 de l'équation complète de l'équation complète
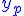 vérifie l'équation vérifie l'équation 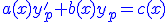 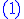
si on ne connaît pas la forme de la solution particulière, on utilise la méthode de la variation de la constante en posant :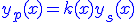
Ce qui permet d'écrire :
En remplaçant dans 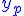 et et 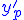 on obtient on obtient
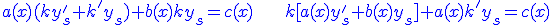
est une équation à variables séparables que l'on sait résoudre
- La solution générale de l'équation différentielle
est la somme de la solution de l'équation sans second membre et de la solution particulière
|
|
|
Exemple corrigé:
Résoudre l'équation différentielle
|
|
|
est une équation linéaire définie sur 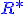
|
- On résout l'équation sans second membre
On obtient
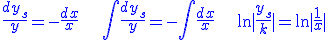
- On cherche une solution particulière de l'équation avec second membre en utilisant la méthode de la variation de la constante
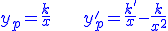
On remplace dans l'équation différentielle avec second membre (1)
On en déduit :
- La solution générale de l'équation différentielle
est la somme de la solution de l'équation sans second membre et de la solution particulière
|
tracés des solutions de l'équation différentielle
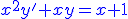
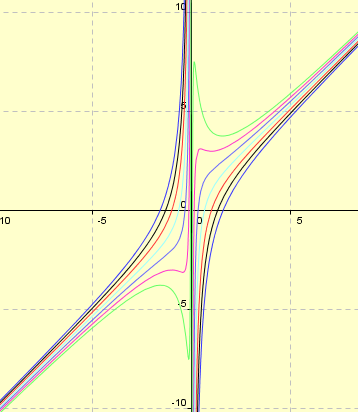
|