Equilibre chimique atmosphère-océans

Un système est considéré comme fermé lorsqu'il ne se produit pas d'échange entre le système lui-même et le milieu extérieur.

Dans l'environnement, une eau souterraine d'une nappe captive ou des eaux océaniques ou lacustres profondes, pour lesquelles le contact avec l'atmosphère est très limité peuvent être considérées comme des systèmes thermodynamiques fermés.

- Système carbonate

Si on considère un système carbonaté fermé tel qu'une eau profonde, les équilibres de dissolution des gaz n'interviennent pas dans la considération des équilibres. Les espèces à prendre en compte dans le cas d'un système carbonate seul sont les espèces en solution H₂CO₃, HCO₃^-, CO₃^2-, ces espèces appartiennent aux couples acide-base suivants : H₂CO₃/ HCO₃^- (pKa₁ = 6,4) et HCO₃^-/CO₃^2- (pKa₂ = 10,3).

Les équilibres acido-basiques qui interviennent dans un tel système sont :

H₂CO₃ + H₂O = HCO₃^- + H₃O⁺ avec

HCO₃^- + H₂O = CO₃^2- + H₃O⁺ avec

Si on considère que la teneur en carbonate total est égale à 10^-3 mol/L, on peut écrire :

A partir des expressions de Ka, on peut écrire :

et

D'où :

soit :

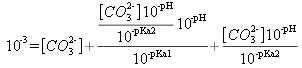
Et :

donc

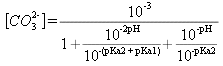
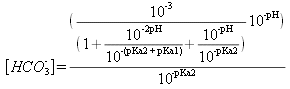et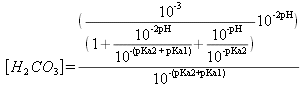

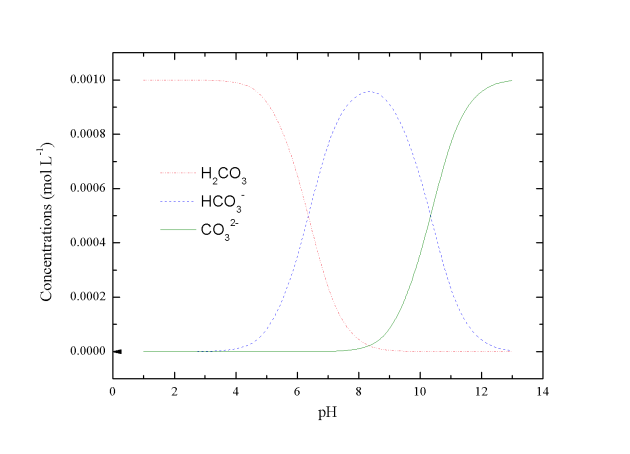
La répartition des différentes formes carbonatées en fonction du pH est donnée dans le graphique 7

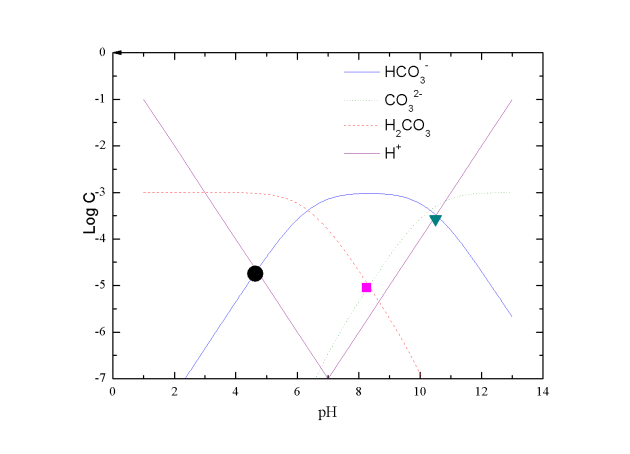
Si on représente le graphique 7 sous la forme log C = f(pH), en rajoutant les droites log [H⁺] = f(pH), on peut en déduire le pH d'une solution de H₂CO₃ (rond noir), de NaHCO₃ (carré rose), ou de Na₂CO₃ (triangle vert) graphique 8.

-Système sulfate

Contrairement à l'exemple que nous venons de traiter dans le cas d'une eau profonde pour laquelle le contact avec un gaz n'est pas favorisé, certains milieux naturels tels que les milieux karstiques par exemple comportent des zones dans lesquelles des échanges avec des quantités finies de gaz sont possibles. Si on considère un tel système, il est nécessaire de connaître la proportion de gaz et d'eau du système. Prenons pour exemple une eau en contact avec un volume fini de SO2(g) et un rapport V_eau/V_tot = 5.10^-4 l/m3. Calculons en fonction du pH de milieu la répartition des différentes formes du soufre dans de telles conditions.

Calculons le volume de gaz : V_gaz = V_tot - V_eau

V_gaz = V_tot – 5.10^-4.V_tot soit V_gaz = 0,9995.V_tot

Le nombre de moles de SO₂(g) est donc soit

La dissolution de SO₂(g) dans l'eau est donnée par la réaction :

SO₂(g) + H₂O(l) = SO₂.H₂O(aq), la constante de Henry de cette réaction est K_H = 1,25.

SO₂.H₂O(aq) est un diacide dont les équilibres de dissociation sont donnés ci-dessous:

SO₂.H₂O(aq) + H₂O(l) = H₃O⁺ + HSO₃^- K₁= 1,29 10^-2

HSO₃^- + H₂O(l) = H₃O⁺ + SO₃^2- K₂ = 6,24 10^-8

Le nombre de moles totales de SO₂ est : n_{SO2 tot}= n_SO2(g)+ n_SO2(l)

Soit: C_{SO2 tot} V_tot= C_SO2(g) V_g+ C_SO2(l) V_l

La concentration en SO₂ totale est alors :

Sachant que , nous pouvons calculer les concentrations en H₂SO₃, HSO₃^- et SO₃^2- grâce aux 3 équilibres précédemment écrits.

D'après la loi de Henry appliquée à la réaction SO₂(g) + H₂O(l) = SO₂.H₂O(aq) , on peut écrire :

. Sachant que on obtient

Pour l'espèce HSO₃^-, on a la réaction SO₂.H₂O(aq) + H₂O(l) = H₃O⁺ + HSO₃^-avec K₁= 1,29 10^-2

D'après cet équilibre, on peut écrire :

Pour l'espèce SO₃^2- on a l'équilibre HSO₃^- + H₂O(l) = H₃O⁺ + SO₃^2-avec K₂ = 6,24 10^-8

Ainsi

En remplaçant dans l'expression de C_SO2tot, on a :

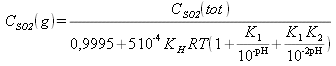
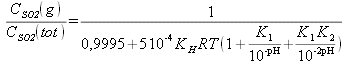
Ainsi, on peut représenter la répartition du soufre entre la phase aqueuse et la phase gazeuse en fonction du pH du milieu.