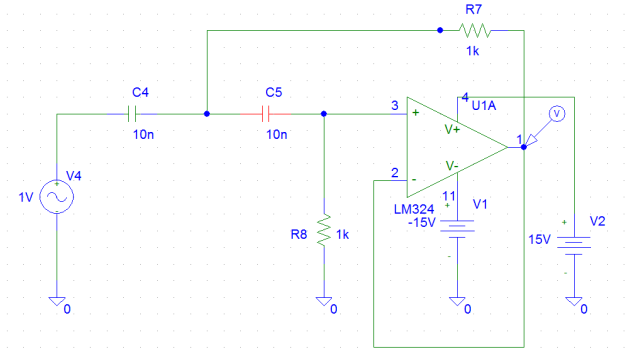
Structure de Sallen-Key
On va se contenter dans ce paragraphe de donner la structure générale de la cellule de Sallen-Key et de traiter un seul exemple, un filtre passe-haut puisque dans le paragraphe précédent, nous avons déjà réalisé un passe-bas et un passe-bande à l'aide de la structure de Rauch. Moyennant un raisonnement analogue à ce qui a été déjà fait plus haut pour la structure de Rauch, on parviendra aisément à réaliser n'importe quel type de filtre à l'aide de la structure Sallen-Key. Ici encore, on laisse le soin au lecteur de tracer le diagramme de Bode à l'aide de scilab et de réaliser la simulation sous Pspice du schéma correspondant.
Le schéma générique est donné par la figure ci-dessous dans laquelle on voit un amplificateur de gain K réalisé par exemple à l'aide du montage classique d'amplificateur inverseur ou non inverseur (cf. chapitre 2) selon qu'on souhaite K négatif ou positif.
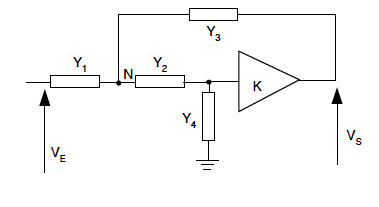
Cellule générique de Sallen-Key
La détermination de la fonction de transfert est aisée en écrivant le théorème de Millman au point N et en remarquant que les admittances 
et 
sont montées en pont diviseur, l'amplificateur de gain K étant idéal, à impédance d'entrée infini (il ne consomme pas de courant) . Ainsi :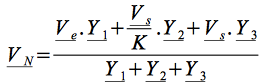 
et 
soit
En introduisant cette dernière expression dans la première, on obtient finalement : 
On obtient un passe-bas, passe-haut, passe-bande ou coupe-bande par un choix judicieux de résistances et condensateurs pour les admittances 
à
.
La fonction de transfert canonique d'un filtre passe-haut du second ordre est :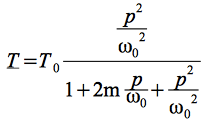 
Remarque :
En toute rigueur, la valeur du gain est obtenue quand la pulsation tend vers l'infini : c'est le gain dans la bande passante. On peut également le noter
.
A présent qu'il est clair et bien assimilé que les admittances sont des quantités complexes, nous abandonnons la notation spécifique avec le souligné en dessous de la quantité pour alléger la notation.
Il vient immédiatement que 
et 
doivent être des condensateurs. Au dénominateur, la seule chance pour avoir le terme réel (1 dans le polynôme duu second degré en p) réside dans le produit 
: il est donc clair que ces deux admittances seront des résistances.
Nous choisissons : 
La cellule de Sallen-Key correspondante est représentée en figure ci-dessous dans laquelle l'amplificateur est un suiveur donc de gain unité.
Moyennant le choix des composants ci-dessus introduit dans la fonction de transfert générique de la cellule, on trouve après calculs : 
puis, par identification assez directe, 
, 
et 
.
Le lien ci-dessous permet de télécharger le schéma PSice d'un filter à structure de Sallen Key.
