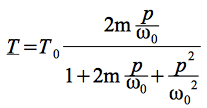Structure de Rauch
Elle est conforme au schéma ci-dessous où les dipôles (résistances et condensateurs) sont représentés via leurs admittances de manière à appliquer le théorème de Millman :
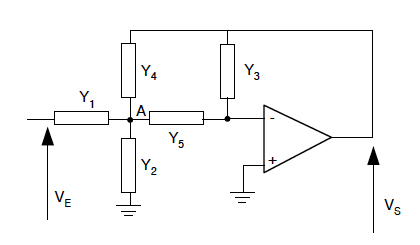
La détermination de la fonction de transfert est aisée en écrivant le théorème de Millman deux fois, au point A et sur l'entrée inverseuse de l'ampli-op qui est au potentiel de la masse puisque l'ampli-op fonctionne en régime linéaire. Ainsi : 
et 
soit
En introduisant cette dernière expression dans la première, on obtient finalement :
On obtient un passe-bas, passe-haut, passe-bande ou coupe-bande par un choix judicieux de résistances et condensateurs pour les admittances
à
.
Par exemple, pour obtenir un passe-bas, il faut que le numérateur soit réel ce qui impose directement et 
réels, soit des résistances. Au dénominateur, la somme 
sera complexe à partie réelle et imaginaire. Pour obtenir un second ordre, il faudra opter pour
imaginaire, c'est-à-dire un condensateur. Du coup, le terme réel au dénominateur est nécessairement apporté par le produit 
ce qui impose 
réel, soit une résistance. Enfin, pour que la somme 
soit complexe à partie réelle et imaginaire, il faut nécessairement que 
soit imaginaire pur, soit un condensateur. Nous avons ainsi déterminé la nature des cinq admittances.
On choisit
et en posant 
comme c'est l'usage,
La fonction de transfert s'écrit alors :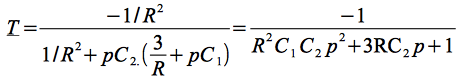 
qu'on met sous la forme canonique :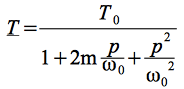 
avec, par identification immédiate, 
, 
et 
.
Remarque :
On peut régler aisément le coefficient m du filtre par réglage des capacités des condensateurs mais alors on modifie la pulsation caractéristique.
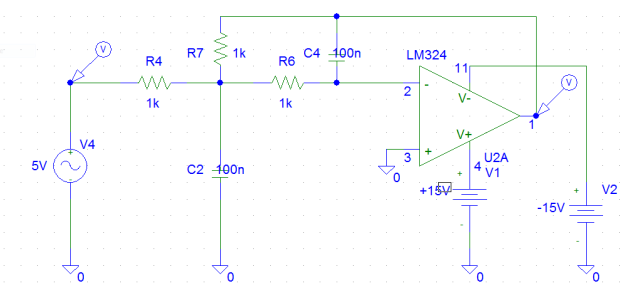
Le schéma Pspice est donné ci-dessous :
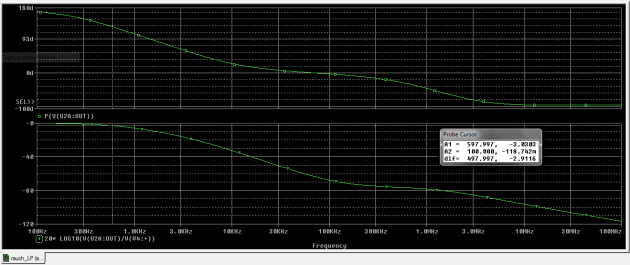
Le diagramme de Bode ci-dessous, tracé sous Scilab, correspond au passe-bas avec 
et
.
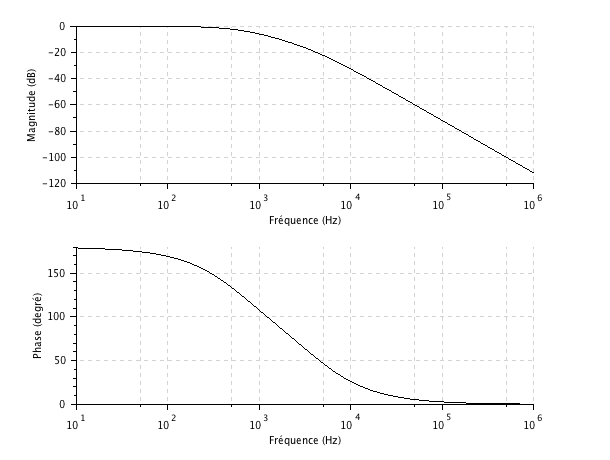
La simulation pscipe est donnée ci-dessous :
Le lien ci-dessous permet de télécharger le schéma PSpice du passe-bas en structure de Rauch.
Les résultats de cette simulation spice diffèrent quelque peu du tracé du diagramme de Bode par scilab. C'est une conséquence des imperfections de l'ampli-op dont le modèle de simulation Pscpice tient compte : au -delà de 100 kHz, l'ampli-op cesse d'être idéal et fait apparaître des imperfections qui modifient la fonction de transfert du second ordre.
A titre d'exercice, on fait la synthèse d'un passe-bande avec une structure de Rauch et on laissera le soin au lecteur d'en faire la simulation Pscipe ou encore d'en tracer le diagramme de Bode théorique par scilab.
La fonction de transfert canonique d'un filtre passe-bande du second ordre est :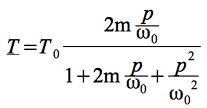 
En mettant cette fonction de transfert canonique en regard de la fonction de transfert générique de la structure de Rauch, 
on peut constater que le numérateur doit être imaginaire pur ce qui impose que 
ou
doit être un condensateur. Au dénominateur, la somme 
sera complexe à partie réelle et imaginaire. Pour obtenir un second ordre, il faudra opter pour 
imaginaire, c'est-à-dire un condensateur. Du coup, le terme réel au dénominateur est nécessairement apporté par le produit 
ce qui impose 
et 
réels, soit des résistances. Comme le produit 
doit être imaginaire pur (cf. supra), on choisit pour 
un condensateur. Dès lors, la somme 
est déjà complexe à partie réelle et imaginaire, on peut donc opter pour une résistance pour 
. Nous avons ainsi déterminé la nature des cinq admittances.
On choisit 
Remarque :
D'autres combinaisons d'admittances (résistances et condensateurs) peuvent également conduire à une fonction de transfert de passe-bas : on laisse au lecteur le soin de le vérifier.
Il reste à identifier les caractéristiques du filtre sous forme canonique aux composants du montage :
La fonction de transfert de la structure de Rauch s'écrit : 
qu'on met sous la forme canonique : 
avec, par identification immédiate, 
, 
et
.
