Diagramme de Bode
Nous faisons un petit retour sur le diagramme de Bode pour mettre notamment en avant les petites subtilités qui apparaissent dans le cas d'un filtrage actif et pour généraliser les notions qui ont été abordées au cours du chapitre précédent.
Comme le filtre est dorénavant actif, le gain peut être quelconque y compris supérieur à 1, à 0 dB en échelle logarithmique. Nous avons déjà vu la notion de fréquence de coupure, c'est-à-dire la ou les fréquences pour lesquelles le gain est diminué de 3 dB par rapport au gain de la bande passante. L'ordre du filtre peut être quelconque supérieur à 2 : on obtient des ordres élevés par cascade de cellules du premier et du second ordre. L'ordre du filtre se traduit en général sur le plan mathématique formel par un polynôme de degré n au dénominateur de la fonction de transfert.
Il faut également comprendre que choisir un filtre correspond à faire un compromis entre une fonction de transfert idéale et la réalité physique qui impose ses contraintes notamment en terme de complexité voire tout simplement de faisabilité. Nous illustrons cette question de compromis sur l'exemple du filtre passe-bas.
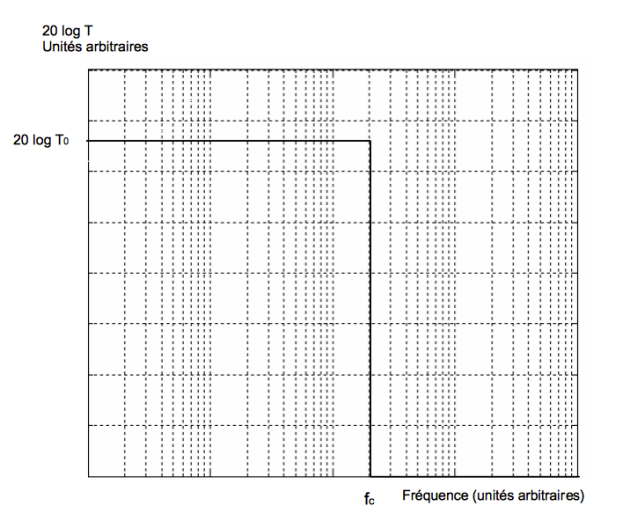
Filtre passe-bas : un passe-bas idéal correspond à laisser passer parfaitement toutes les fréquences (avec éventuellement un gain dans cette bande passante) et à rejeter parfaitement toutes les fréquences supérieures à la fréquence de coupure. Du point de vue du diagramme de Bode, en amplitude pour l'instant, ça correspond à ce gabarit idéal, aisé à comprendre :
Toutefois, on montre, qu'un tel filtre n'est pas réalisable physiquement en temps réel. Un des problèmes que pose cette fonction de transfert idéale est la verticale à la fréquence de coupure. En réalité, avec un circuit réel, on peut obtenir une pente raide, d'autant plus raide que l'ordre du filtre sera élevé, mais sans jamais toutefois obtenir une pente verticale. Plus l'ordre du filtre est élevé, plus le circuit sera complexe puisqu'il faudra cascader plusieurs cellules du premier et second ordre. On comprend d'ores et déjà pourquoi, le concepteur de filtre sera toujours amené à adopter un compromis entre le cahier des charges et les contraintes de la faisabilité physique.
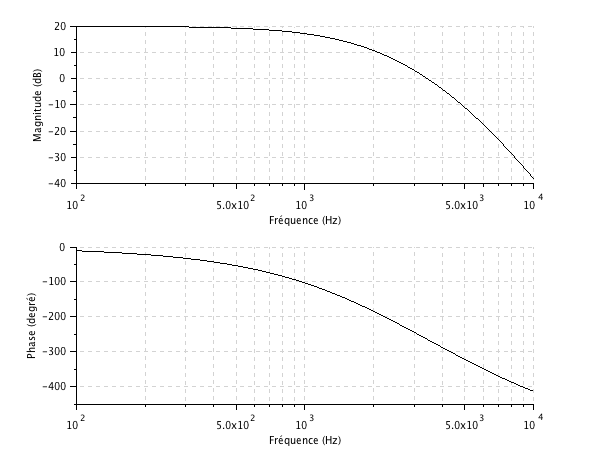
La figure ci-dessous représente le diagramme de Bode d'un passe-bas du sixième ordre réalisable physiquement en cascadant trois cellules du second ordre avec un gain de 20 dB dans la bande passante. On y voit que la fréquence de coupure (à 20 db – 3 dB) est aux alentours de 1 kHz. Un tel filtre du sixième ordre possède une atténuation de 120 db par décade (- 20 dB par décade pour un premier ordre, soit 6 fois – 20 dB par décade pour un sixième ordre).