Étude du mouvement
Référentiel : géocentrique (centre
de la Terre), supposé galiléen.Système : le satellite de masse
.Forces : force
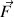d'attraction gravitationnelle.
Application de la deuxième loi de Newton :
Le satellite est soumis à la force gravitationnelle centripète
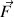exercée par la Terre de masse
:
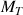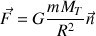
On a donc :
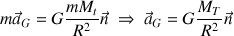
Le vecteur accélération est centripète et sa valeur est constante : le mouvement circulaire est donc uniforme de vitesse
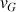telle que :
Quand on parle de l'altitude
d'un satellite, on parle de la distance du satellite à la surface de la Terre. Si on appelle
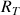le rayon de la Terre, on a :
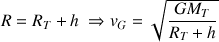
Remarque :
Dans le référentiel géocentrique, le mouvement du centre d'inertie d'un satellite en orbite circulaire est uniforme. Sa vitesse n'est fonction que de son altitude
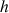. Elle diminue lorsque l'altitude augmente. La vitesse est indépendante de la masse du satellite.
La période de révolution
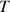, c'est-à-dire la durée pour effectuer un tour, est égale au rapport de la circonférence de l'orbite sur la vitesse orbitale :
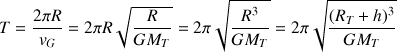
Ainsi on voit que la période d'un satellite augmente avec son altitude.
On a aussi :
Fondamental :
C'est la troisième loi de Kepler, la loi des périodes, où, pour un mouvement circulaire, le demi-grand axe
est égal au rayon
.
