Primitives
Soit la fonction
dépendant de la position
et du temps
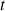. On dit que la fonction
est une primitive d'une fonction
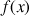, si la dérivée de
correspond à
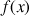, c'est-à-dire si :
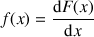
Soit la fonction
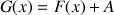, où
est une constante. On a :
Ainsi, les fonctions
,
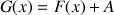ou
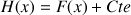sont toutes des primitives de
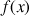: une primitive n'est connue qu'à une constante près.
Les primitives qui vont nous intéresser dans ce chapitre sont :
la primitive de
la primitive de
Exemple :
1 – Calculer la primitive de
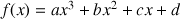
2 – Calculer la primitive de
3 – Calculer la primitive de
-------------------------------
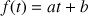
1 – La primitive de
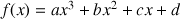est :
2 – La primitive de
est :
3 – La primitive de
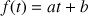est :
