Dérivées
Soit la fonction
dépendant de la position
et du temps
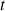. En mathématiques, la dérivée d'une fonction correspond à la variation de cette fonction en fonction d'une de ses variables. Ainsi on peut écrire :
• la dérivée spatiale :
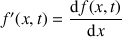
• la dérivée temporelle :
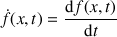
Si
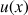et
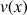sont deux fonctions de la variable
, on a :
Exemple :
1 – Calculer la dérivée de
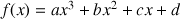
2 – Calculer la dérivée de
------------------------------
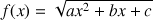
1 – La dérivée de :
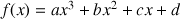est
2 – La dérivée de :
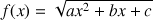est :
