Relations de conjugaison
A partir de la construction géométrique précédente, il est possible d'établir les formules géométriques qui expriment la dépendance de l'image (position, nature et sens) en fonction de l'objet.
Soient I le point d'intersection entre la lentille et le rayon incident parallèle à l'axe et le J le point d'intersection entre la lentille et le rayon émergent parallèle à l'axe.
Les triangles (JOF) et (JIB) sont semblables et de même pour (IOF') et (IJB'). On en déduit
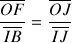et
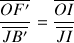
En ajoutant terme à terme les deux équations précédentes, en remarquant
et
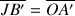et sachant que
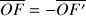, on obtient la relation de Descartes.
Fondamental : La relation de Descartes
La relation de conjugaison des lentilles minces avec origine au centre optique de la lentille s'écrit :
Cette relation détermine algébriquement la position de l'image en fonction de celle de l'objet et de la distance focale de la lentille.
Elle permet aussi de déterminer la nature de l'image :
, l'image est réelle
, l'image est virtuelle
Il est possible d'établir une relation entre la position de l'objet et de l'image en prenant comme origine des mesures algébriques les foyers et non le centre.
Complément : Relation de Newton
Il s'agit de la relation de conjugaison avec origine aux foyers.
