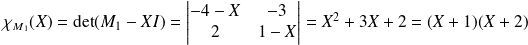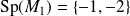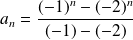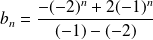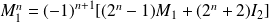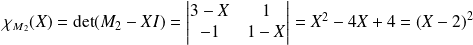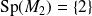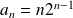Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
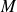une matrice de
.
Question
Montrer que, pour tout
, il existe
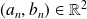tels que
.
Utilisez la division euclidienne de
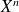par le polynôme caractéristique de
.
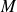Le polynôme caractéristique de
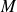est un polynôme de degré 2 :
.
Pour tout entier
, par division euclidienne de
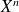par
, il existe deux polynômes
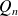et
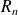tels que
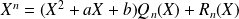et
.
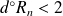Donc, pour tout entier
, il existe des réels
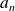et
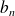tels que
.
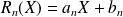Donc :
.
Or d'après le théorème de Cayley-Hamilton,
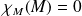, donc
.
Conclusion : Pour tout entier
, il existe des réels
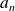et
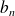tels que
.
Question
Calculer
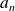et
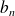en fonction des valeurs propres de
.
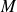Séparez en deux cas selon le nombre de valeurs propres de
.
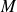Le polynôme caractéristique est de degré 2, donc il y a deux cas : dans
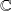, soit il a deux racines distinctes (et la matrice
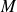a deux valeurs propres), soit il a une racine double réelle (et la matrice
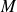a une seule valeur propre).
Si
avec
:
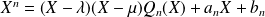.Donc
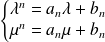.Conclusion :
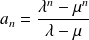et
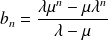si
.
Si
:
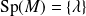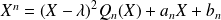.Et en dérivant :
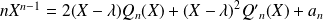.Donc
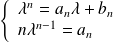.Conclusion :
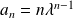et
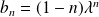si
.
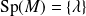