A Roland Garros
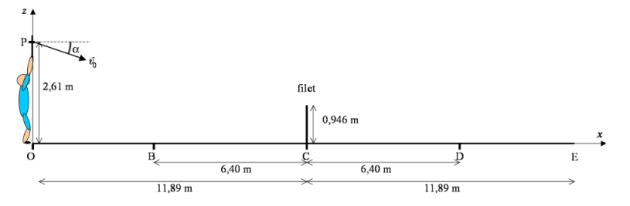
Au tennis, un service est correct si la balle touche le sol derrière le filet sur une distance allant du filet jusqu'à 6,40 m, c'est-à-dire, par rapport au schéma, qu'une balle frappée par un joueur en P à la verticale de O doit toucher le sol entre C et D. De plus, une balle de tennis a un rayon de 3,2 cm, et elle ne doit pas toucher le filet qui est haut de 0,914 m ; donc le centre d'inertie de la balle doit passer au moins à 0,946 m au-dessus du sol lorsqu'elle passe le filet.
On considère que la trajectoire de la balle se passe dans un plan vertical
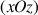. On négligera les frottements de l'air. La balle est touchée au point P situé à
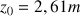à la verticale de A avec la vitesse initiale
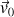et faisant un angle
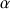avec l'horizontale. On prendra pour l'accélération de la pesanteur
.
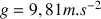Question
La balle est jugée bonne si elle touche le sol entre C et D. Quelles sont les abscisses
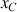et
?
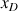D'après le schéma, on voit de manière évidente :
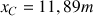et
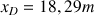
Question
Donner les composantes de la vitesse
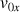et
.
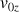D'après le schéma, on a les composantes du vecteur vitesse initiale
:
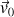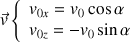
Question
Établir les équations horaires
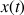et
.
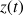Le système étudié ici est la balle de tennis (repérée par son centre d'inertie G). Pour faire l'étude de son mouvement on choisit de prendre un référentiel terrestre (supposé galiléen). Les forces qui agissent sur le système sont :
- le poids
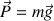
- les frottements de l'air sur la balle, mais qui sont négligés (voir énoncé).
Il s'agit donc d'un mouvement de chute libre.
On applique la 2ème loi de Newton sur le système :
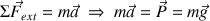
Le vecteur accélération
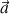du centre d'inertie de la balle est donc :
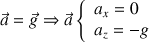
Le vecteur accélération correspond à la variation du vecteur vitesse :
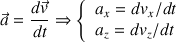
Pour obtenir les coordonnées du vecteur vitesse
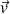, on part des coordonnées du vecteur accélération :
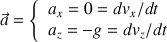
On intègre les équations différentielles pour trouver les coordonnées du vecteur vitesse :
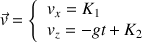
On doit évaluer les constantes
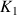et
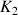. Les coordonnées du vecteur vitesse doivent être exactes même pour
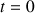. D'après la relation ci-dessus, on a :
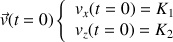
Or d'après l'énoncé, le ballon est lancé avec une vitesses initiale
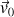faisant un angle
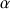avec l'horizontale, soit :
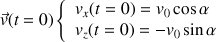
On identifie alors :
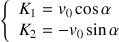
Ce qui donne pour les coordonnées du vecteur vitesse :
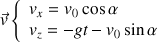
Le vecteur vitesse correspond à la variation du vecteur position :
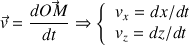
Pour obtenir les coordonnées du vecteur position
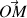, on part des coordonnées du vecteur vitesse :
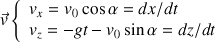
On intègre les équations différentielles pour trouver les coordonnées du vecteur position :
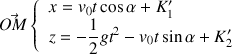
On doit évaluer les constantes
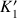et
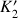. Les coordonnées du vecteur position doivent être exactes même pour
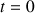. D'après la relation ci-dessus, on a :
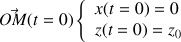
On identifie alors :
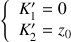
Ce qui donne pour les coordonnées du vecteur position :
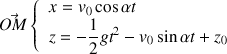
Question
En déduire l'équation de la trajectoire dans le plan
.
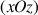Pour écrire l'équation de la trajectoire, il faut éliminer le temps entre les composantes du vecteur position. n utilise la composante
pour exprimer le temps sous la forme :
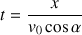
On peut alors remplacer le terme temporel de la composante
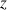par celui que l'on vient d'écrire :
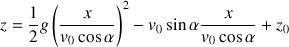
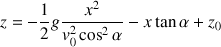
On obtient une expression qui ne dépend plus du temps.
Question
De l'équation précédente, exprimer la vitesse
.
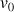De l'équation de la trajectoire, on obtient :
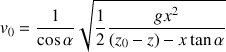
Question
L'angle de départ est
.
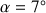a) Quelle doit être la vitesse
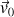pour que la balle touche le sol en D ? Passe t-elle au dessus du filet sans le toucher ?
b) Quelle doit être la vitesse
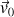pour que la passe juste au-dessus du filet ? Touche t-elle le sol entre C et D (pour vous aider, vous pouvez exprimer l'équation du second degré en x avec ses valeurs numériques) ?
Avec un angle de départ
.
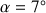a) On veut
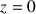à
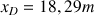, soit pour :
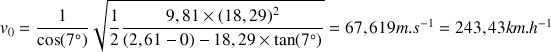
Avec cette vitesse, à la distance
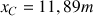, la hauteur de la balle est de :
La hauteur de la balle est supérieure à la hauteur de
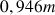: elle passe au-dessus du filet.
b) On veut
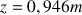à
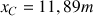, soit pour :
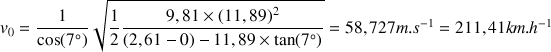
Si elle touche le sol, on a
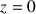pour
donnée par :
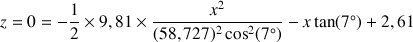
soit l'équation du second degré :
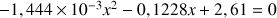
On résout cette équation du deuxième degré en calculant le discriminant :
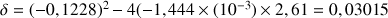
et les deux racines :
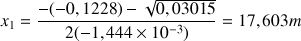
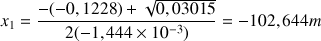
Seule la position positive est à retenir, soit
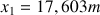, et elle se trouve entre
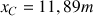et
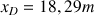. La balle touche bien le sol dans les limites.
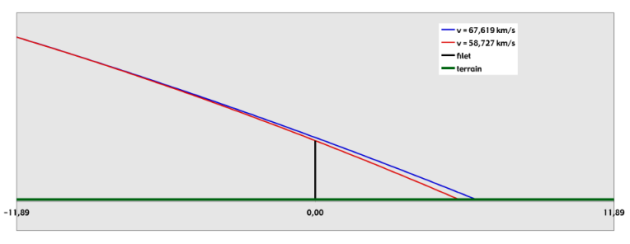
On peut schématiser les deux situations comme ceci :
