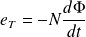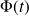Théorie
1. Notion de force électromotrice
1.1. Définition
Considérons une charge ponctuelle q soumise à une force
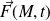, susceptible de parcourir une courbe fermée C. On appelle force électromotrice présente dans le circuit à l'instant t la grandeur :
Cette expression correspond à la circulation, le long du contour fermé C, du vecteur
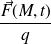. D'un point de vue dimensionnel, e(t) est homogène à une tension électrique et s'exprime en volts.
Concrètement, c'est la force
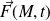qui engendre le mouvement de la charge q le long du contour et par là même un courant d'intensité I. Si le contour est un conducteur matériel de résistance R, le courant créé s'exprimera par : e(t) = RI.
1.2. Cas des champs permanents
Appliquons alors ce concept à la force de Lorentz électromagnétique exercée sur les porteurs de charges mobiles d'un conducteur filiforme :
Plaçons nous enfin dans le cadre des régimes stationnaires où le champ électrique
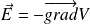et dans le cas d'un conducteur immobile dans le référentiel d'étude. La vitesse
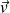représentant la vitesse d'un porteur par rapport au conducteur, est évidemment colinéaire à
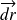. Alors e(t)=0 car le deuxième terme est nul et la circulation de
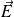est conservative.
En régime stationnaire et pour un conducteur immobile, la force de Lorentz est conservative : elle ne peut engendrer de fém dans un circuit. |
Dans la suite, nous envisageons des situations expérimentales où l'une au moins de ces conditions citées ci-dessus n'est pas respectée à savoir le régime stationnaire et le circuit immobile. Nous observerons dans ce cas, l'apparition dans le circuit d'une force électromotrice (fèm) engendrant un courant appelé courant induit. Cette fem est aussi obtenue par la circulation non nulle d'un champ
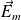le long du circuit fermé appelé champ électromoteur.
2. Mises en évidence expérimentales
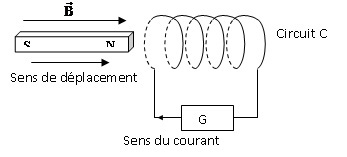
En déplaçant un aimant dans le circuit fermé C (Bobine à N spires) schématisé ci-dessous, on soumet ce circuit à un champ
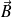dépendant du temps. Pendant le déplacement de l'aimant, on assiste au passage d'un courant dans un sens bien déterminé, qui d'ailleurs s'inverse quand on éloigne l'aimant. Nous observons que l'amplitude du courant dépend de la vitesse de déplacement de l'aimant, et donc de la rapidité de variation de
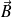. Elle dépend aussi du nombre de spires formant la bobine et de leur surface.
Mais il est possible également de laisser l'aimant fixe (donc le champ B est permanent) et de déplacer le circuit C : on observe le même phénomène car relativement, les différents points du circuit voient toujours un champ
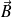variable.
Le phénomène important étant donc le déplacement relatif de l'aimant par rapport à la bobine. La première expérience illustre cependant le cas d'un régime non stationnaire et la deuxième le cas d'un circuit mobile.
De ces expériences et de nombreuses autres, Faraday (1831) et Lenz (1834) ont déduit des lois expérimentales exprimant la fem qui apparaît dans le circuit, encore appelée fem induite .
3. Résultats expérimentaux
3.1. Loi de Faraday
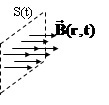
Elle relie la fem e(t) à la variation temporelle du flux magnétique qui traverse le circuit :
le flux magnétique
|  |
Cette expression décrit bien les effets observés expérimentalement : fem due à une variation de flux, d'autant plus importante que le flux varie rapidement.
3.2. Loi de Lenz
La loi de Lenz est qualitative : elle explicite le signe - de la loi de Faraday :
La fem induite tend par ses effets à s'opposer à la cause qui l'a créée |
Si on revient à l'exemple ci-dessus, chaque spire est traversée par le flux variable et est le siège d'une fém induite
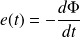. La fém totale est donc donnée par :
