Détermination de l'indice en fonction de la longueur d'onde
 | Atelier goniomètre : détermination de la variation de l'indice en fonction de la longueur d'onde |
Nous avons mis en évidence dans l'étude de la déviation en fonction de l'angle d'incidence un minimum de déviation correspondant à un angle du prisme donné et une longueur d'onde donnée.
En mesurant pour chaque longueur d'onde de la lampe spectrale , la déviation minimum nous obtenons la valeur de l'indice grâce à la relation:
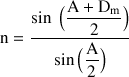
où A est l'angle du prisme et Dm la déviation minimum. Nous obtiendrons alors un tableau de valeurs faisant correspondre à chaque longueur d'onde une valeur de l'indice:
Longueur d'onde (nm) | indice n |
643,8 | 1,7169 |
579,1 | 1,7243 |
577,0 | 1,7247 |
546,1 | 1,7297 |
508,5 | 1,7374 |
481,1 | 1,7436 |
479,4 | 1,7437 |
472,2 | 1,7463 |
468,0 | 1,7471 |
435,8 | 1,7567 |
407,4 | 1,7674 |
Nous utiliserons le tableur Excel et son solveur pour déterminer la meilleure relation reliant la longueur d'onde à l'indice n en évaluant par moindres carrés quelques relations susceptibles de répondre au problème:
,
,
,
Voici le début du tableau réalisé sous Microsoft Excel:
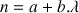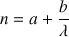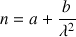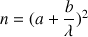
Vous évaluerez les constantes a et b en utilisant le modèle pour 2 couples de valeurs (n , ).
Vous porterez ces valeurs dans les cases a et b (moindres carrés) , puis vous exprimerez le modèle en cellule C11 par: $C$6+$C$7*A11 que vous appliquerez aux cellules C12 à C21
Vous calculerez ensuite les moindres carrés en exprimant la cellule D11 par: (C10-B10)^2 que vous appliquerez aux cellules D12 à D21.
Vous calculerez ensuite la somme des moindres carrés en C23 par: SOMME(D11,D21)
Vous lancerez ensuite le solveur (s'il n'est pas dans le menu "Outils" de excel il faudra l'installer en cliquant sur "Macros complémentaires" et en cochant "Complément solver") qui se présente ainsi:
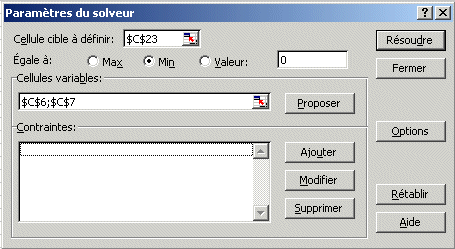
Dans la cellule cible à définir vous pointerez sur la cellule contenant la somme des moindres carrés: $D$23, vous cocherez la case "min" car on veut minimiser cette somme; enfin dans cellules variables on mettrales cellules contenant les paramètres que l'on veut ajuster (a et b) c'est-à-dire $C$6 et $C$7.On cliquera alors sur "Résoudre" pour obtenir les paramètres a et b qui minimisent la somme des moindres carrés.Vous répéterez ces opérations pour les différents modèles retenus et vous en déduirez la relation qui se rapproche le plus des valeurs expérimentales (par minimisation de la somme des moindres carrés).
