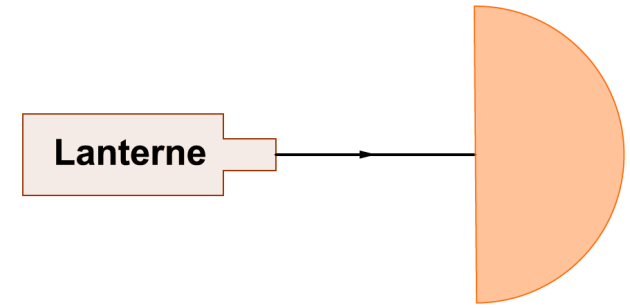
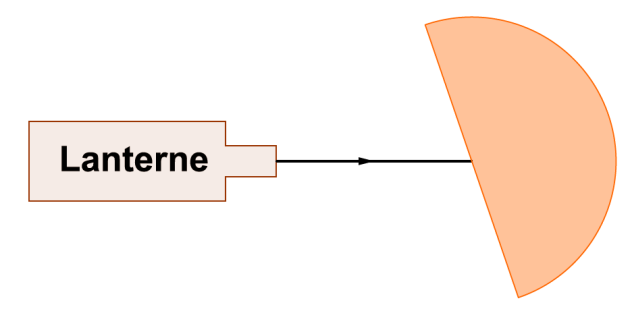
Réfraction sur un dioptre plan air/Plexiglas
1. Disposer le demi-cylindre sur la feuille de sorte que la face plane se superpose avec l'axe des 90°. Veiller à ce que le centre de demi-cylindre coïncide avec le centre du cercle trigonométrique.
2. Faire en sorte que le rayon incident arrive perpendiculairement à la face plane du demi-cylindre en passant par son centre.
Que peut-on dire du rayon réfracté ? Compléter le schéma en ajoutant le(s) rayon(s) observé(s).
3. Tourner le demi-cylindre (avec la feuille) de sorte à faire varier l'angle d'incidence sans faire varier le point d'incidence.
Que peut-on observer ? Compléter le schéma en ajoutant le(s) rayon(s) observé(s) ainsi que les angles d'incidence,de réfraction et de réflexion.
4. Faire varier l'angle d'incidence \(i_1\) et noter les valeurs de l'angle de réfraction \(i_2\) correspondant dans le tableau ci-dessous (les angles étant exprimés en radians). Sur la feuille A3, dessiner au crayon les rayons observés ainsi que les angles d'incidence et de réfraction.
\(i_1\) | \(i_2\) | \(sin(i_1)\) | \(sin(i_2)\) | \(sin(i_1)/sin(i_2)\) |
. | ||||
. | ||||
. | ||||
. | ||||
. |
5. Tracer sur un même graphique les courbes \(i_1 = f(i_2)\) et \(sin(i_1) = f (sin(i_2))\).
Vérifier que pour les petits angles, les courbes sont tangentes.
6. Ecrire la loi de Descartes. Que représente la pente de la droite \(sin(i_1) = f (sin(i_2))\) ?
En déduire la valeur de l'indice de réfraction du plexiglas sachant que l'indice de l'air vaut 1.
7. Donner à l'angle d'incidence la plus grande valeur possible (préciser laquelle). Observer la disposition des couleurs du rayon réfracté à l'aide d'une feuille blanche placée à une distance qu'il faudra ajuster. Que peut-on en déduire concernant l'indice de réfraction du plexiglas ?
Illustration du phénomène à observer par une animation :