Applications de classe C k
Dans ce qui suit,
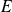 et
et
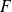 sont des
sont des
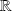 - espaces vectoriels normés de dimension finie,
- espaces vectoriels normés de dimension finie,
 est un ouvert non vide de
est un ouvert non vide de
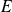 et
et
 est une application de
est une application de
 dans
dans
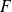 .
.
Définition :
La fonction
 est continûment différentiable ou de classe
est continûment différentiable ou de classe
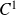 en
en
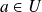 si
si
 est différentiable en
est différentiable en
 et si sa différentielle
et si sa différentielle
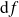 est continue en
est continue en
 .
.
La fonction
 est continûment différentiable ou de classe
est continûment différentiable ou de classe
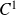 sur
sur
 si
si
 est différentiable sur
est différentiable sur
 et si sa différentielle
et si sa différentielle
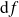 est continue sur
est continue sur
 .
.
La différentielle de
 est une application de
est une application de
 dans
dans
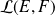 qui est de dimension finie.
qui est de dimension finie.
Il s'agit donc de montrer que :
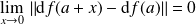 pour n'importe quelle norme.
pour n'importe quelle norme.
Fondamental :
Propriétés
La fonction
 est de classe
est de classe
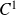 sur
sur
 si et seulement si toutes ses coordonnées dans une base de
si et seulement si toutes ses coordonnées dans une base de
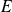 le sont.
le sont.La fonction
 est de classe
est de classe
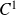 sur
sur
 si et seulement si
si et seulement si
 est différentiable sur
est différentiable sur
 et si pour tout
et si pour tout
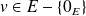 , sa dérivée
, sa dérivée
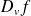 est continue sur
est continue sur
 .
.La fonction
 est de classe
est de classe
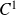 sur
sur
 si et seulement si
si et seulement si
 admet des dérivées partielles sur
admet des dérivées partielles sur
 et si ces dérivées partielles sont continues sur
et si ces dérivées partielles sont continues sur
 .
.
C'est ce dernier critère qui sera le plus facile à utiliser.
Fondamental :
Opérations
Si
 et
et
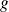 sont de classe
sont de classe
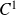 sur
sur
 , alors la fonction
, alors la fonction
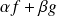 est de classe
est de classe
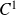 sur
sur
 pour tout
pour tout
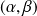 .
.Si
 est de classe
est de classe
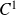 sur
sur
 et si
et si
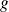 est de classe
est de classe
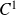 sur un ouvert
sur un ouvert
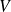 contenant
contenant
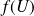 , alors
, alors
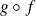 est de classe
est de classe
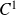 sur
sur
 .
.
Si
 admet des dérivées partielles, chacune d'elles est une application de
admet des dérivées partielles, chacune d'elles est une application de
 dans
dans
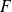 .
.
Elle peut donc elle-même admettre ou non des dérivées partielles.
On en déduit des dérivées partielles successives et des classes de fonctions par récurrence.
Définition :
La fonction
 est de classe
est de classe
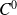 sur un ouvert
sur un ouvert
 non vide si
non vide si
 est continue sur
est continue sur
 .
.
Pour tout
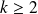 ,
,
 est de classe
est de classe
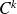 sur
sur
 si
si
 est de classe
est de classe
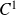 sur
sur
 et si ses dérivées partielles sont de classe
et si ses dérivées partielles sont de classe
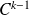 sur
sur
 .
.
Si
 est de classe
est de classe
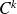 , on définit ses dérivées partielles d'ordre
, on définit ses dérivées partielles d'ordre
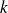 :
:
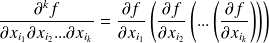 .
.
La fonction
 est de classe
est de classe
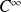 si elle est de classe
si elle est de classe
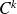 pour tout entier
pour tout entier
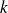 .
.
Exemple : La fonction
 définie par :
définie par :
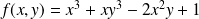 admet des dérivées partielles d'ordre
admet des dérivées partielles d'ordre
 .
.
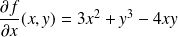 et
et
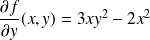 .
.
Ces fonctions admettent aussi des dérivées partielles qui sont les dérivées partielles d'ordre
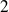 de
de
 .
.
En dérivant par rapport à
 :
:
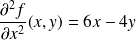 , et :
, et :
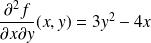 .
.
En dérivant par rapport à
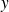 :
:
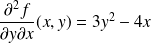 , et :
, et :
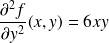 .
.
Si l'on dérive encore, on obtient les dérivées partielles d'ordre
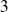 de
de
 :
:
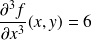 ,
,
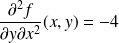 ,
,
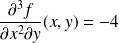 et
et
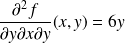 .
.
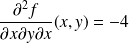 ,
,
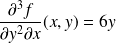 ,
,
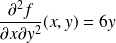 et
et
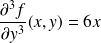 .
.
Fondamental :
Propriétés
L'ensemble des fonctions de classe
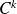 sur
sur
 est un espace vectoriel et :
est un espace vectoriel et :
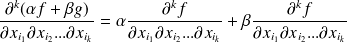 .
.Le produit de deux fonctions de classe
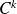 sur un ouvert non vide
sur un ouvert non vide
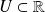 est une fonction de classe
est une fonction de classe
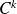 sur
sur
 .
.Si la fonction
 est de classe
est de classe
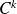 sur un ouvert non vide
sur un ouvert non vide
 de
de
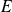 à valeurs dans un ouvert
à valeurs dans un ouvert
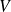 de
de
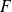 et si
et si
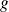 est une fonction de classe
est une fonction de classe
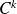 sur
sur
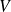 , alors la fonction
, alors la fonction
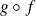 est de classe
est de classe
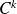 sur
sur
 .
.
Dans l'exemple précédent, on peut remarquer que :
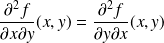 .
.
Et donc :
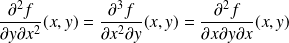 .
.
De même :
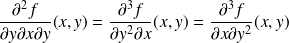 .
.
Pour cette fonction, l'ordre des dérivations n'a pas d'importance. C'est le cas des fonctions de classe
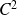 sur un ouvert.
sur un ouvert.
Fondamental :
Théorème de Schwarz
Si
 est de classe
est de classe
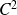 sur un ouvert
sur un ouvert
 non vide, alors :
non vide, alors :
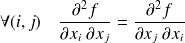 .
.
On peut utiliser ce théorème pour démontrer qu'une fonction n'est pas de classe
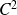 .
.
Il suffira de trouver deux variables telles que :
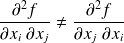 .
.





