Généralités
Les fonctions considérées sont des fonctions définies sur un intervalle de
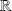et à valeurs dans un espace vectoriel normé
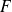de dimension finie.
Définition :
Une équation différentielle d'ordre
est une relation entre la variable
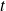, une fonction
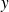et ses dérivées
, ...,
:
.
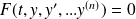On dira que l'équation différentielle est "résolue" en
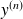si elle peut se mettre sous la forme :
.
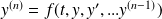Par exemple, l'équation
:
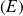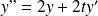est une équation différentielle d'ordre
résolue en
.
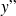Définition :
On appelle solution de l'équation différentielle sur un intervalle
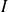de
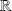toute fonction
fois dérivable sur
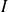qui vérifie l'équation.
La courbe représentative d'une solution est appelée courbe intégrale de l'équation différentielle.
Une fonction
est donc une
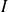- solution de l'équation différentielle si elle est
fois dérivable sur
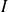et si :
.
Résoudre l'équation différentielle sur un intervalle
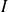de
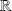, c'est trouver toutes les
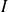- solutions de l'équation.
Par exemple, la fonction
définie par :
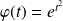est solution sur
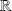de l'équation précédente :
.
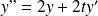Mais il n'y a pas unicité puisque toute fonction de la forme
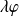(avec
) est aussi solution.
Définition :
On appelle condition initiale la donnée en un point
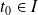des valeurs de la solution
et de ses dérivées.
Problème de Cauchy : Il s'agit de déterminer les solutions de l'équation différentielle sur l'intervalle
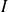qui vérifient une condition initiale donnée.
La condition initiale est donc la donnée de
.
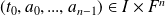Et il s'agit de déterminer les
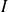- solutions de l'équation qui vérifient :
.
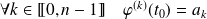Dans l'exemple précédent, la fonction
définie par :
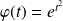vérifie la condition initiale :
.
