Compacité
Dans ce qui suit,
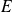désigne un espace vectoriel normé sur
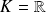ou
.
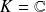Définition :
Une partie
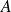de
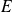est compacte si toute suite d'éléments de
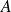admet au moins une valeur d'adhérence dans
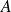, c'est-à-dire s'il existe une suite extraite qui converge dans
.
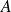Par exemple un segment
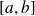est une partie compacte de
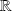, mais
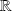n'est pas compact car de la suite de terme général
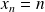, on ne peut pas extraire une suite convergente.
Fondamental :
Propriétés :
L'intersection d'un nombre fini ou infini de parties compactes est une partie compacte.
La réunion d'un nombre fini de parties compactes est une partie compacte.
Un produit
de parties compactes d'espaces vectoriels normés
, ...,
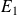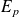est une partie compacte de
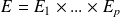muni de la norme produit.
Par exemple,
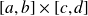est un compact de
.
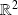Fondamental :
Toute partie compacte de
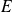est fermée et bornée.En dimension finie, une partie de
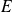est compacte si et seulement si elle est fermée et bornée.Toute partie compacte de
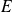est complète.
Fondamental :
Si
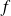est une application continue d'un espace vectoriel normé
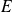dans un espace vectoriel normé
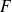et si
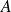est un compact de
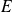, alors
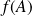est un compact de
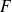.Si
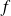est une application continue d'un espace vectoriel normé
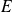dans
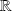et si
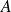est un compact de
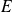, alors
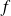est bornée sur
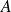et atteint ses bornes.
