Cas des fonctions à valeurs complexes
Les fonctions considérées sont à valeurs complexes, définie sur un intervalle
de
.
Définition :
Si
est une fonction à valeurs complexes sur
,
est intégrable si ses parties réelle et imaginaire sont intégrables et :
.
En particulier, sont intégrables sur
les fonctions à valeurs complexes continues par morceaux sur
, c'est-à-dire dont les parties réelle et imaginaire sont continues par morceaux sur
.
Fondamental :
Conséquences :
.
. 
.
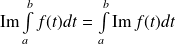Fondamental :
Théorème fondamental
Si
est une fonction continue par morceaux sur un intervalle
et si
, alors la fonction
est l'unique primitive de
sur
qui s'annule en
.
Conséquence :
pour toute primitive
de
sur
.
Les propriétés des intégrales de fonctions réelles s'étendent aux fonctions complexes sauf celles qui concernent la relation d'ordre.
Fondamental :
Linéarité
Si
et
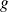sont deux fonctions continues par morceaux sur
:
.
Si
est une fonction continue par morceaux sur
et si
est un complexe :
.
Relation de Chasles
Si la fonction
est continue par morceaux sur un intervalle
, alors :
.
Intégration par parties
Si
et
sont
par morceaux sur
:
.
Changement de variable
si
est continue par morceaux sur
, si
est de classe
sur
et si
.
Pour les inégalités, seules restent les inégalités sur les modules.
Fondamental :
Si
une fonction continue par morceaux sur un intervalle
avec
, alors :
.
Inégalité de Cauchy-Schwarz
Si
et
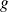sont deux fonctions continues par morceaux sur un intervalle
, alors :
.
Il y a égalité si et seulement si les deux fonctions sont liées.
