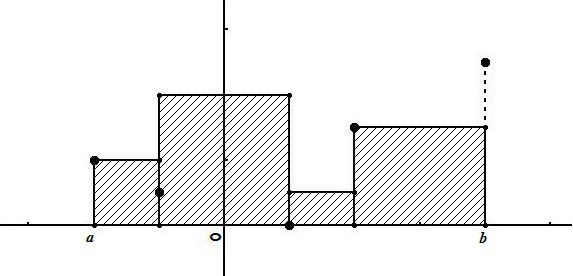
Fonctions en escalier
Soit
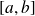un segment de
tel que
.
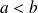Les fonctions considérées sont définies sur
et à valeurs réelles.
Définition :
Une subdivision du segment
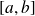est une suite strictement croissante
où
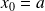et
.
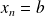Le pas de la subdivision est :
.
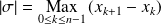La subdivision est régulière si tous les segments sont de même longueur :
.
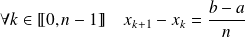Définition :
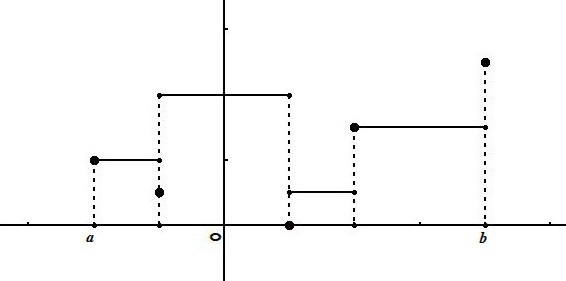
Une fonction
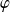est une fonction en escalier sur
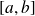s'il existe une subdivision
de
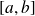pour laquelle
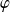est constante sur
pour tout
:
.
On dira que la subdivision
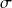est adaptée à la fonction en escalier
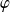sur
.
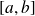Une telle subdivision n'est évidemment pas unique.
Fondamental :
Si
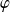est une fonction en escalier sur
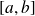, la somme
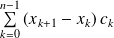est indépendante de la subdivision
adaptée à
.
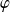Cette somme est l'intégrale de
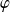sur
:
.
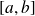On peut remarquer que la valeur de l'intégrale ne dépend pas des valeurs prises par la fonction
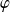aux points de la subdivision.
Et la variable
est une variable muette :
.
Fondamental :
Interprétation géométrique
Si
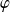est une fonction en escalier à valeurs positives sur
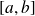, l'intégrale
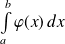est l'aire de la partie de plan limitée par la courbe représentative de
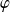, l'axe des abscisses et les droites d'équations
et
.
