Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
 la fonction définie par :
la fonction définie par :
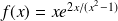 .
.
Question
Déterminer les limites de la fonction
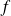 aux bornes de son ensemble de définition.
aux bornes de son ensemble de définition.
Interprétez géométriquement.
Utilisez la composition des limites et les équivalents.
La fonction
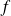 est définie sur :
est définie sur :
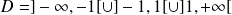 .
.
Etude en
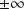 :
: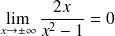 . Donc :
. Donc :
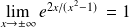 . Donc :
. Donc :
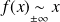 .
.Conclusion :
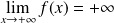 et
et
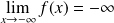 .
.On étudie l'existence d'une asymptote :
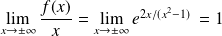 .
.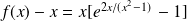 et
et
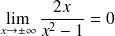 . Donc :
. Donc :
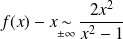 .
.Donc :
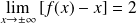 .
.Conclusion : La courbe représentative de la fonction
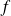 admet en
admet en
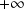 et en
et en
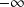 une asymptote oblique d'équation
une asymptote oblique d'équation
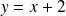 .
.Etude en
 :
: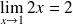 et
et
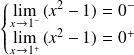 .
. Donc :
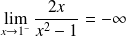 et
et
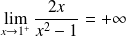 .
.Donc :
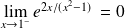 et
et
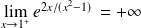 .
.Conclusion :
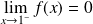 et
et
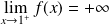 .
.La courbe représentative de la fonction
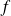 admet à gauche de
admet à gauche de
 un point limite
un point limite
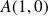 et à droite de
et à droite de
 une asymptote verticale d'équation
une asymptote verticale d'équation
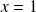 .
.Etude en
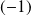 :
: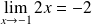 et
et
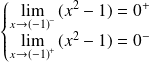 .
. Donc :
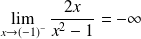 et
et
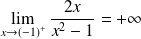 .
.Donc :
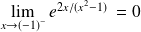 et
et
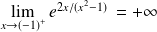 .
.Conclusion :
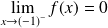 et
et
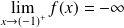 .
.La courbe représentative de la fonction
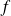 admet à gauche de
admet à gauche de
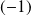 un point limite
un point limite
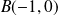 et à droite de
et à droite de
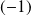 une asymptote verticale d'équation
une asymptote verticale d'équation
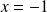 .
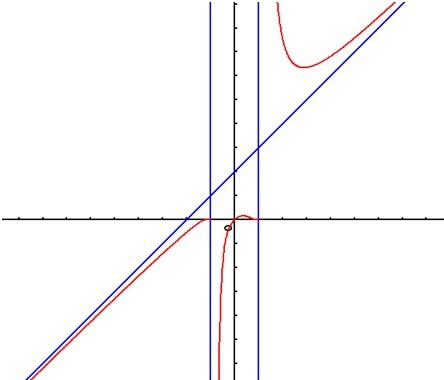
.Allure de la courbe (après étude des variations) :