Extension aux fonctions à valeurs complexes
Soit
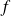 une fonction définie sur un intervalle
une fonction définie sur un intervalle
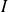 de
de
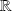 et à valeurs complexes.
et à valeurs complexes.
On lui associe deux fonctions à valeurs réelles définie sur le même intervalle.
Définition :
La fonction
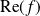 :
:
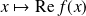 est la partie réelle de
est la partie réelle de
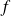 .
.
La fonction
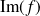 :
:
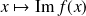 est la partie imaginaire de
est la partie imaginaire de
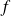 .
.
La définition d'une limite finie s'étend aux fonctions complexes en remplaçant la valeur absolue par le module.
Définition :
La fonction
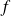 admet en
admet en
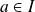 (réel) une limite complexe
(réel) une limite complexe
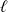 si :
si :
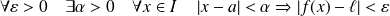 .
.
La fonction
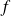 admet en
admet en
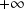 une limite complexe
une limite complexe
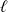 si :
si :
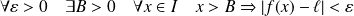 .
.
La fonction
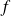 admet en
admet en
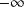 une limite complexe
une limite complexe
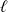 si :
si :
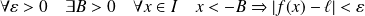 .
.
Fondamental :
La fonction
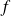 admet en
admet en
 (réel ou infini) une limite finie si et seulement ses parties réelles et imaginaires admettent en
(réel ou infini) une limite finie si et seulement ses parties réelles et imaginaires admettent en
 des limites réelles.
des limites réelles.
Si
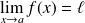 , alors
, alors
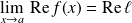 et
et
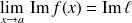 .
.
Réciproquement, si
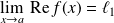 et
et
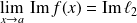 , alors
, alors
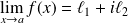 .
.
Par contre, les notions de
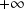 et de
et de
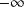 n'ont pas de sens dans le corps des complexes.
n'ont pas de sens dans le corps des complexes.
Définition :
La fonction
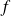 admet en
admet en
 une limite infinie si sa partie réelle ou sa partie imaginaire admet en
une limite infinie si sa partie réelle ou sa partie imaginaire admet en
 une limite infinie.
une limite infinie.
Les propriétés des limites réelles s'étendent aux limites finies de fonctions complexes sauf celles qui concernent la relation d'ordre.
Fondamental :
Opérations algébriques
Soient
 et
et
 deux fonctions qui admettent en
deux fonctions qui admettent en
 des limites finies
des limites finies
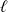 et
et
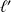 .
.
Leur somme
 admet en
admet en
 une limite finie :
une limite finie :
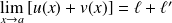 .
.Leur produit
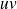 admet en
admet en
 une limite finie :
une limite finie :
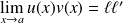 .
.Leur quotient
 admet en
admet en
 une limite finie si
une limite finie si
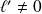 :
:
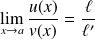 .
.
Composition
Si
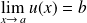 (réel) et si
(réel) et si
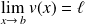 (complexe), alors
(complexe), alors
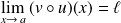 .
.
Fondamental :
Caractérisation séquentielle d'une limite (
 réel ou infini)
réel ou infini)
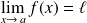 si et seulement si, pour toute suite
si et seulement si, pour toute suite
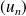 convergeant vers
convergeant vers
 , la suite
, la suite
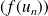 converge vers
converge vers
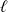 .
.





