Limite en un point
Soit
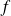une fonction définie sur un intervalle
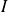de
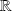et à valeurs réelles.
La fonction
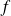est définie au voisinage d'un réel
si
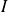contient au moins un intervalle de la forme
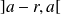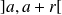ou
où
est un réel strictement positif.
Définition :
Limite réelle en un point
Soit
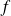une fonction définie au voisinage d'un réel
.
La fonction
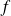admet en
une limite réelle
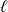si :
.
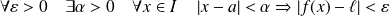Cette limite, si elle existe, est unique et l'on note :
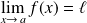ou
.
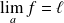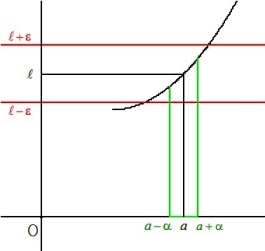
On peut rendre
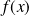aussi proche que l'on veut de
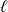à condition de prendre
suffisamment proche de
.
Pour tout
compris entre
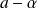et
,
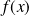est compris entre
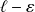et
.
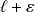Remarques
Si
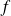est définie en
, la seule limite possible est :
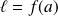.Si
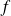admet une limite réelle en
, alors
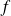est bornée au voisinage de
.
Fondamental :
Interprétation géométrique
Si
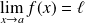, la courbe représentative de
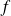admet un « point limite »
.
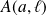On obtient le coefficient directeur de la tangente en
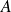en étudiant la limite en
de
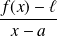si elle existe.
Définition :
Limite infinie en un point
Soit
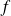une fonction définie au voisinage d'un réel
.
La fonction
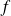admet en
la limite
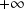si :
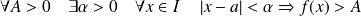.On note :
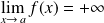ou
.
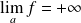La fonction
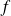admet en
la limite
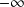si :
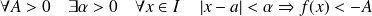.On note :
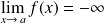ou
.
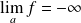Pour la limite
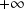, on peut rendre
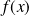aussi grand que l'on veut à condition de prendre
suffisamment proche de
.
Pour tout
compris entre
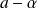et
,
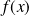est plus grand que
.
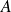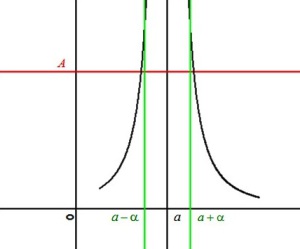
Fondamental :
Interprétation géométrique
Si
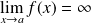, la courbe représentative de
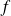admet une droite « asymptote verticale » d'équation
.
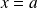On note :
.
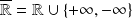Définition :
Limites à gauche et à droite
Soit
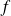une fonction définie au voisinage d'un réel
.
Une fonction
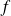admet en
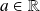une limite à gauche
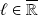si la restriction de
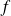à
a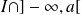dmet la limite
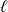.Les définitions s'obtiennent en remplaçant
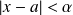par
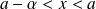.Cette limite, si elle existe, est notée :
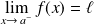ou
.
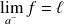Une fonction
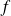admet en
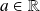une limite à droite
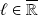si la restriction de
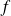à
a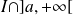dmet la limite
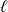.Les définitions s'obtiennent en remplaçant
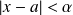par
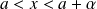.Cette limite, si elle existe, est notée :
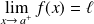ou
.
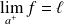Si la fonction
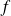est définie à gauche et à droite de
, elle admet une limite en
si et seulement si elle admet une limite à gauche et une limite à droite en
et si ces deux limites sont égales.
Une fonction peut admettre en
une limite à gauche et une limite à droite, sans admettre de limite en
.
On étudie alors séparément les comportements à gauche et à droite. Il peut y avoir deux points limites ou un point limite et une asymptote verticale.
