Cas des autres séries
On essaie de se ramener à l'étude d'une série à termes positifs.
Lorsqu'une série
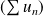 est à termes négatifs, il suffit de considérer la série
est à termes négatifs, il suffit de considérer la série
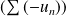 .
.
Dans les autres cas, on fait appel à la valeur absolue.
Définition :
Une série
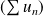 est absolument convergente si la série
est absolument convergente si la série
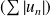 est convergente.
est convergente.
Fondamental :
Propriétés
Si la série
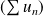 est absolument convergente, alors elle est convergente et :
est absolument convergente, alors elle est convergente et :
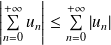 .
.On ne modifie pas la somme d'une série absolument convergente en modifiant l'ordre des termes.
Mais la réciproque est fausse : une série peut être convergente sans être absolument convergente.
Par exemple, la série
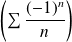 est convergente alors que la série
est convergente alors que la série
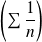 est divergente.
est divergente.
Définition :
Une série est semi convergente si elle est convergente mais pas absolument convergente.
Définition :
Le produit de Cauchy des séries
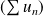 et
et
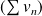 est la série de terme général :
est la série de terme général :
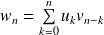 .
.
Fondamental :
Propriété
Si les séries
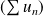 et
et
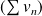 sont absolument convergentes, leur produit de Cauchy
sont absolument convergentes, leur produit de Cauchy
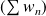 est absolument convergent.
est absolument convergent.
Alors :
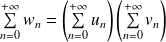 .
.
Une série est alternée si
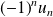 est de signe constant pour tout
est de signe constant pour tout
 .
.
Fondamental :
Cas des séries alternées
Si
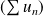 est une série alternée, si la suite
est une série alternée, si la suite
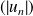 est décroissante et si
est décroissante et si
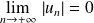 , alors la série
, alors la série
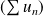 est convergente.
est convergente.
Les suites
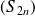 et
et
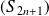 sont adjacentes et
sont adjacentes et
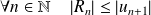 .
.





