Séries de réels
Définition :
Si
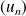est une suite de réels, la série
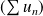est la suite de terme général :
.
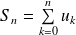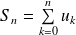est la somme partielle d'ordre n de la série.
Définition :
La série
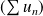est convergente si la suite
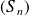converge.
Si la série converge, sa somme est :
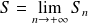, que l'on note :
.
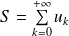Si la série converge, le reste d'ordre n de la série est :
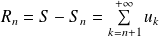. Donc :
.
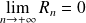La série
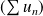est divergente si la suite
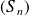diverge.
Etudier la nature d'une série, c'est étudier sa convergence ou sa divergence.
La nature d'une série ne change pas en modifiant un nombre fini de termes.
Fondamental :
Si la série
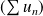converge, alors
.
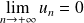Si
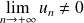, on dira que la série
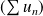diverge « grossièrement ».
Attention :
Attention ! La réciproque de ce théorème est fausse.
Il existe des séries divergentes qui vérifient :
.
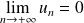Par exemple, la série
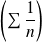est divergente, et pourtant son terme général tend vers
.
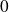Fondamental :
Propriétés :
L'ensemble des séries convergentes est un espace vectoriel et l'application
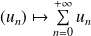est linéaire.Si
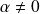, les séries
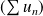et
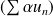sont de même nature.Si
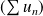converge et
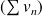diverge, la série
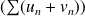diverge.
On ne peut rien dire de la somme de deux séries divergentes.
On peut définir une série de complexes de la même manière qu'une série de réels.
Fondamental :
Une série
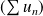de complexes converge si et seulement si les séries
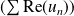et
convergent.
