Suites de complexes
Définition :
Une suite
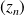de complexes est convergente s'il existe un complexe
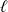tel que :
.
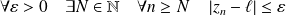S'il existe, ce complexe
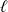est unique. C'est la limite de la suite
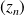et il est noté :
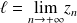ou plus simplement
.
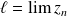Une suite
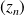de complexes est divergente si elle n'est pas convergente.
Par contre, la notion de suite qui diverge vers
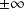n'a plus de sens.
Fondamental :
Les propriétés vues sur les suites de réels sont vraies pour les suites de complexes SAUF celles qui concernent la relation d'ordre.
On ne pourra pas parler de suites monotones ou de suites adjacentes.
Donc pour démontrer une convergence, on ne dispose ni du théorème de convergence monotone ni du théorème d'encadrement.
Fondamental :
Sous forme algébrique
Une suite
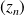de complexes est convergente si et seulement si la suite
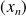des parties réelles et la suite
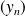des parties imaginaires sont convergentes.
Si
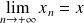et
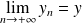, alors
.
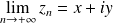Fondamental :
Sous forme trigonométrique
Une suite
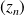de complexes non nuls est convergente si et seulement si :
soit la suite
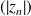converge vers
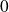,soit la suite
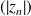converge vers un réel
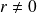et la suite
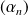des arguments converge.
Dans le premier cas :
.
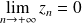Dans le deuxième cas, si
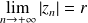et
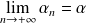, alors
.
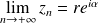